Ballistic Pendulum

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
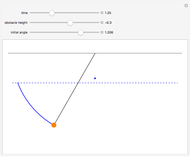
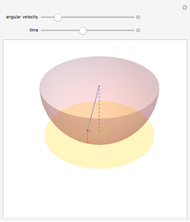
A gun shoots a bullet of mass  into a wooden sphere of mass
into a wooden sphere of mass  . The sphere hangs from a fixed point; the bullet makes the sphere swing up to a height
. The sphere hangs from a fixed point; the bullet makes the sphere swing up to a height  , here taken as 0.1 meters. The bullet has an initial kinetic energy
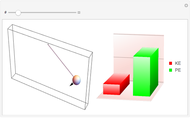
, here taken as 0.1 meters. The bullet has an initial kinetic energy 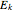 ; when it hits the sphere their kinetic energies are combined. As they swing up together, the kinetic energy is converted into potential energy. In order to make the sphere go up to 0.1 m, the velocity of the bullet must vary. Its velocity can be deduced using the conservation of energy. Vary the mass of the sphere and see how the velocity of the bullet must change in order to maintain the same velocity of the pendulum.
; when it hits the sphere their kinetic energies are combined. As they swing up together, the kinetic energy is converted into potential energy. In order to make the sphere go up to 0.1 m, the velocity of the bullet must vary. Its velocity can be deduced using the conservation of energy. Vary the mass of the sphere and see how the velocity of the bullet must change in order to maintain the same velocity of the pendulum.
Contributed by: Enrique Zeleny (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The velocity of the sphere and the bullet is  and the initial velocity of the bullet is
and the initial velocity of the bullet is 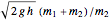 , where
, where  is the acceleration due to gravity,
is the acceleration due to gravity,  is the maximum height of the sphere and
is the maximum height of the sphere and  and
and  are the masses of the bullet and the wood sphere, respectively. You can derive these expressions as an exercise.
are the masses of the bullet and the wood sphere, respectively. You can derive these expressions as an exercise.
Permanent Citation