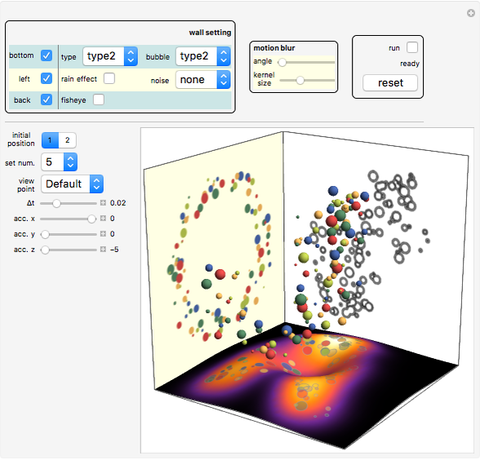
Balls Bouncing off Walls

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
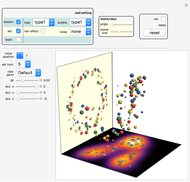
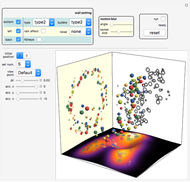
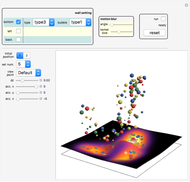
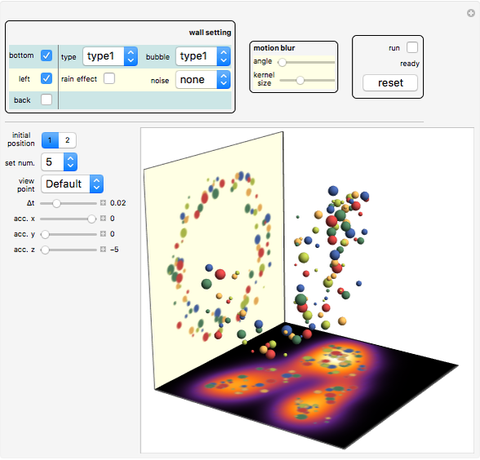
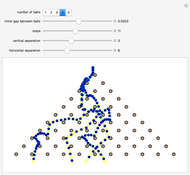
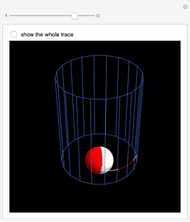
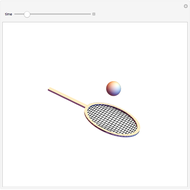
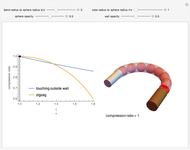
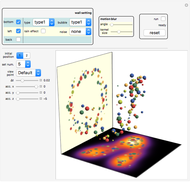
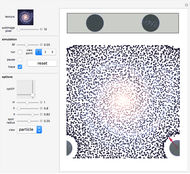
The patterns here are suggested by collisions of colored balls according to the laws of mechanics. Balls with diverse sizes and colors fall under the influence of customizable acceleration due to gravity. They can hit up to three projection walls and bounce back. If a ball leaves the cube, it disappears. Balls interact only with the walls but not with one another. There are several effects that you can set for the projection walls.
Contributed by: Yiyang Li (June 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The collision between a ball 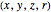 and a projection wall surface
and a projection wall surface 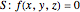 changes only the velocity vector component along the normal direction at the point of collision
changes only the velocity vector component along the normal direction at the point of collision 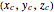 on
on 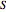 . Before the collision, if the ball's velocity vector is
. Before the collision, if the ball's velocity vector is  and the unit normal at
and the unit normal at 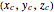 is
is 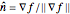 , then
, then  can be written as
can be written as  where
where  and
and  . After collision, the velocity vector becomes
. After collision, the velocity vector becomes 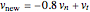 . If the projection wall surface
. If the projection wall surface 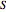 is a plane, then determining an accurate collision point
is a plane, then determining an accurate collision point 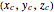 is easy; but if
is easy; but if 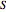 is curved surface, this can be somewhat time-consuming and yields little benefit since the ball's radius is relatively small when compared to the simulation region. Therefore to calculate more quickly, we simply use the sphere center's coordinate
is curved surface, this can be somewhat time-consuming and yields little benefit since the ball's radius is relatively small when compared to the simulation region. Therefore to calculate more quickly, we simply use the sphere center's coordinate 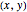 and a
and a 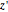 that is obtained by solving the equation
that is obtained by solving the equation  as the point of collision.
as the point of collision.
When a ball hits more than one wall at once, we treat the multiple collisions as follows: if all walls are planes, we write 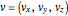 and change it to
and change it to 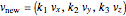 where
where 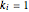 or
or  according to which collision happens along the
according to which collision happens along the  direction. If a wall is a curved surface, then we first deal with the collision on this surface alone using the method described in the previous paragraph and then deal with the remaining collisions on the plane walls.
direction. If a wall is a curved surface, then we first deal with the collision on this surface alone using the method described in the previous paragraph and then deal with the remaining collisions on the plane walls.
This Demonstration is inspired by "Create Unique Charts with Different Visualizations" and "Use Symbolic Graphics Primitives to Visualize Results".A few videos of this Demonstration can be downloaded from the author's personal page.
Possible Issue
The reset button may flicker once after it is clicked, but this does not cause any trouble.
Permanent Citation