Band Spectrum in a Periodic Potential
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
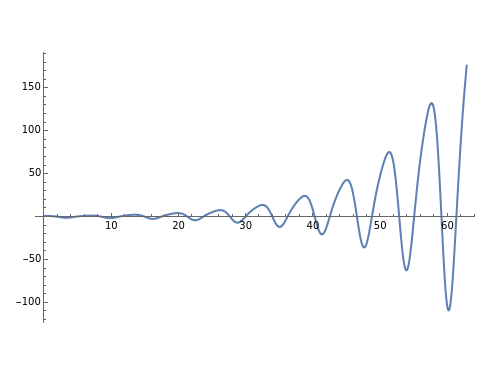
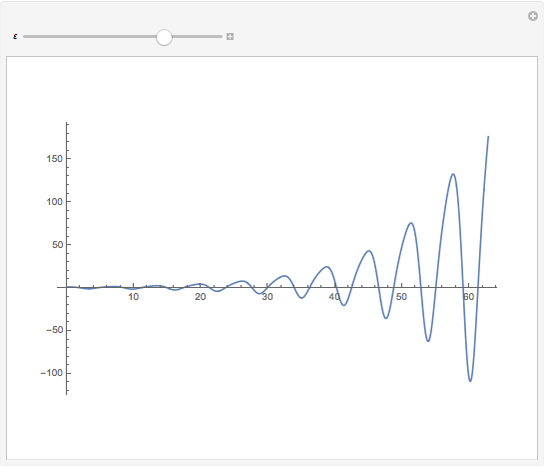
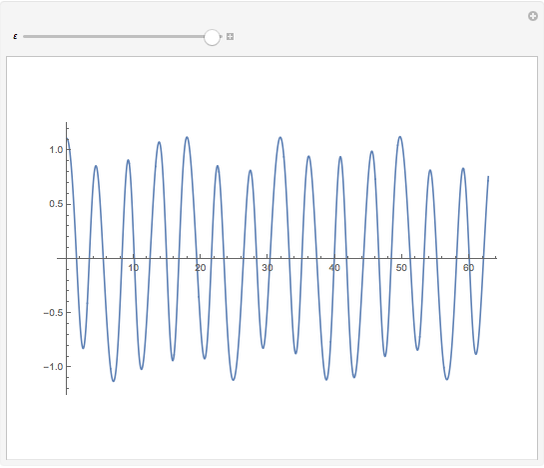
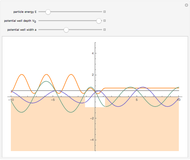
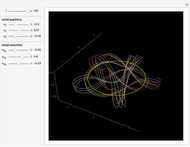
Plot of the symmetric solution of 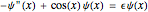 .
.
Contributed by: Michael Trott (January 2011)
Open content licensed under CC BY-NC-SA
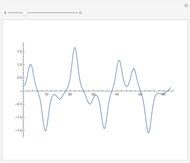
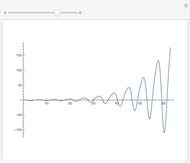
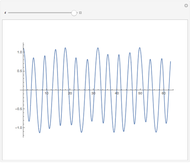
Snapshots
Details
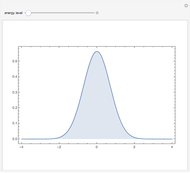
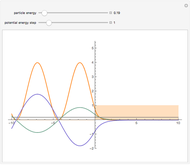
 is the energy.
is the energy.
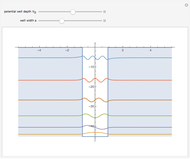
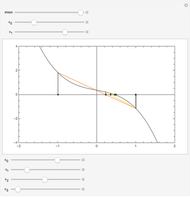
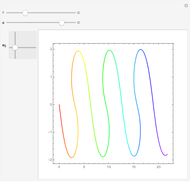
The spectrum of the Schrödinger operator with a periodic potential has allowed energy bands. When the energy is within a band, the eigenfunctions are the product of a phase factor of magnitude 1 and periodic parts. As a result, the eigenfunctions are  ‐normalizable. When the energy is outside the bands, the eigenfunctions grow unbounded as
‐normalizable. When the energy is outside the bands, the eigenfunctions grow unbounded as 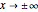 . You can see both situations by varying the energy.
. You can see both situations by varying the energy.
Permanent Citation