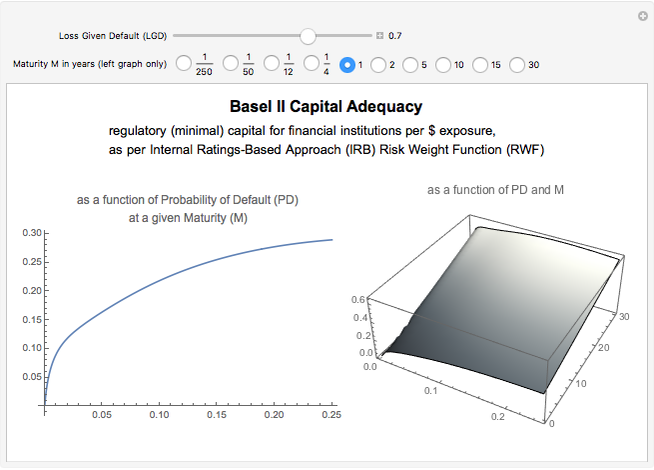
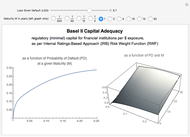
Basel II Capital Adequacy: Internal Ratings-Based (IRB) Approach

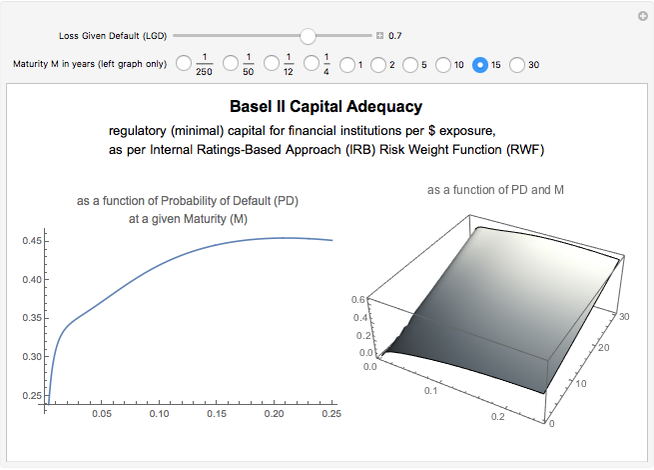
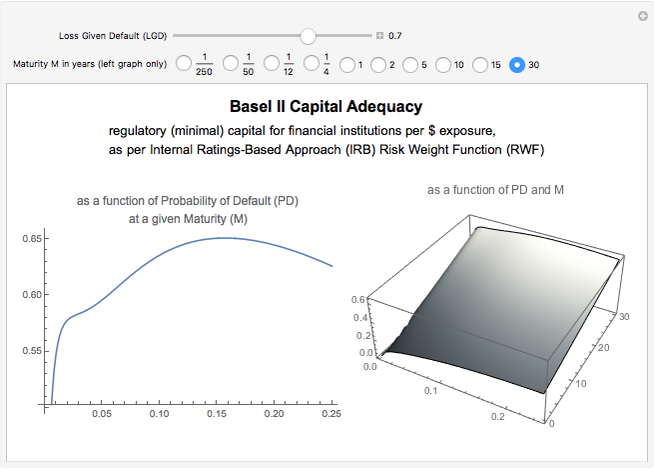
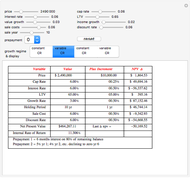
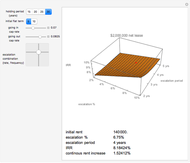
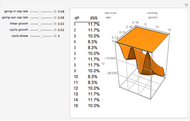
The key cornerstone of prudential regulation of banks (and financial institutions in general) is to ensure that each bank holds sufficient equity capital to absorb unexpected losses, that is, the materialization of financial risks, principally market (price), liquidity, credit, and operational risks.

The so-called Basel II capital adequacy framework introduces a regulatory formula (Risk Weight Function, or RWF) that calculates how much minimum capital the bank must hold for each credit-risky asset, using the bank's own Probability of Default (PD) estimate for said credit-risky asset as the principal input. Because such PD estimates are generally based on the bank's internal credit rating system, this element of Basel II is referred to as the Internal Ratings-Based Approach (IRB).

The Basel II IRB-RWF thus codifies a greatly simplified credit portfolio model, whereby each individual asset's contribution to the portfolio credit risk is additive, homogeneous within each class of assets, and constructed by way of using a Gaussian copula to proxy dependency between credit defaults and the (dire/downturn) state of economy. The parametrization of this RWF is hard-coded, as per Basel Committee on Banking Supervision (BCBS), an international standard setting body based in Basel, Switzerland.