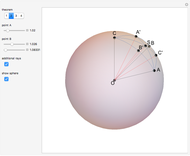
Basis for Pure Geodetic Angles

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
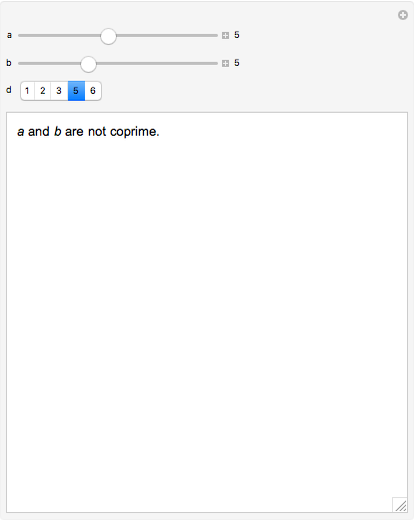
This Demonstration illustrates the theorem: If 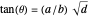 , with square-free positive integer
, with square-free positive integer  and relatively prime
and relatively prime 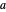 and
and  , and if the prime factorization of
, and if the prime factorization of 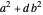 is
is 
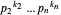 , then we have
, then we have  for some rational
for some rational  .
.
Contributed by: Izidor Hafner (April 2011)
Open content licensed under CC BY-NC-SA
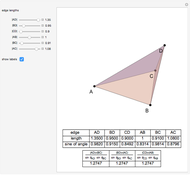
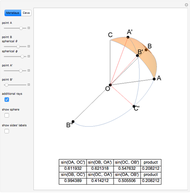
Snapshots
Details
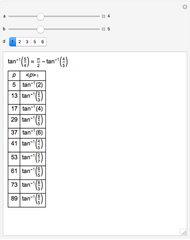
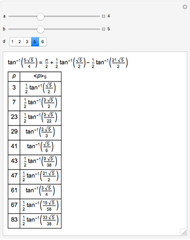
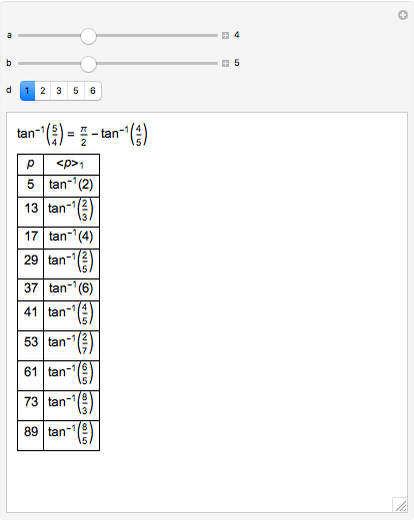
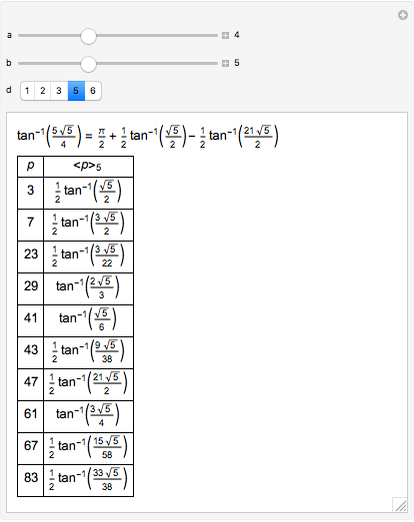
If  is a square-free positive integer and
is a square-free positive integer and  and
and  are integers, then linear combinations of angles with tangents of the form
are integers, then linear combinations of angles with tangents of the form 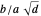 (called pure geodetic angles) form a vector space over the rationals. A basis for the space is formed by
(called pure geodetic angles) form a vector space over the rationals. A basis for the space is formed by 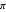 and certain angles
and certain angles for prime
for prime 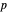 . If
. If 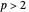 or if
or if 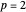 and
and 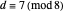 , then
, then  is defined only when
is defined only when 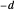 is congruent to a square modulo
is congruent to a square modulo 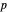 . Express
. Express  as
as 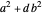 for the smallest possible positive
for the smallest possible positive  . Then
. Then  . Rational linear combinations of pure geodetic angles for all
. Rational linear combinations of pure geodetic angles for all  are called mixed geodetic angles. With fixed
are called mixed geodetic angles. With fixed  we get a vector subspace in the space of all mixed geodetic angles.
we get a vector subspace in the space of all mixed geodetic angles.
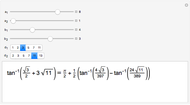
An application: For the dihedral angle 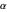 of a dodecahedron we have
of a dodecahedron we have 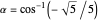 , so
, so 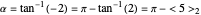 . This means that
. This means that 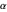 is linearly independent of
is linearly independent of  . If
. If 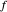 is an additive function over the reals, such that
is an additive function over the reals, such that 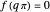 ,
,  rational, we could choose
rational, we could choose 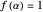 . The Dehn invariant of the dodecahedron is
. The Dehn invariant of the dodecahedron is 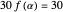 , while for a cube it is
, while for a cube it is 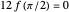 . So the dodecahedron is not equidecomposable with the cube.
. So the dodecahedron is not equidecomposable with the cube.
Reference
[1] J. H. Conway, C. Radin, and L. Sadun, "On Angles Whose Squared Trigonometric Functions Are Rational," Discrete & Computational Geometry, 22(3), 1999 pp. 321–332.
Permanent Citation