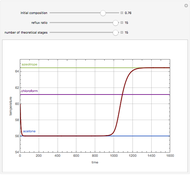
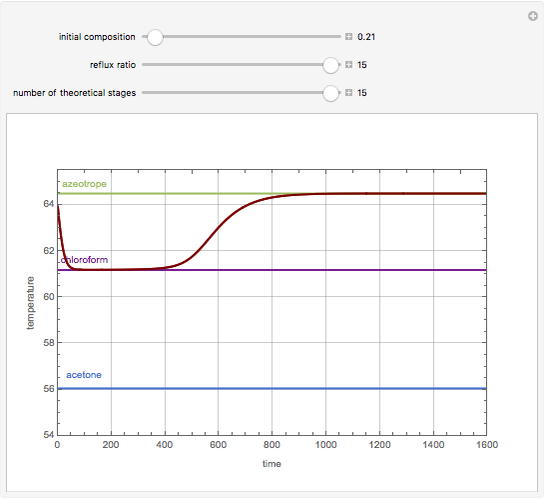
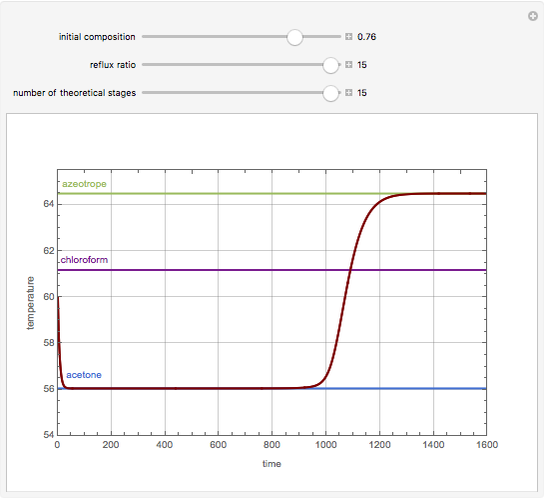
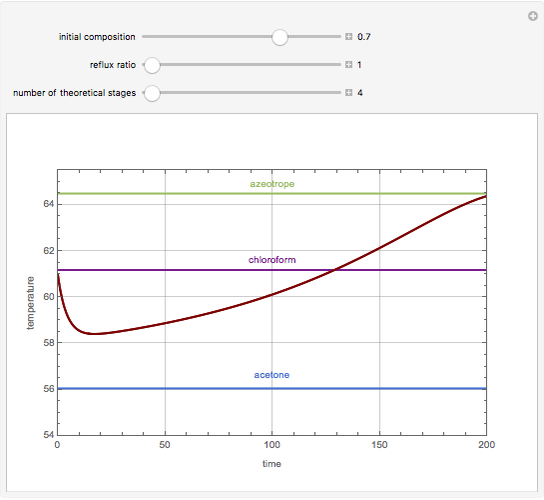
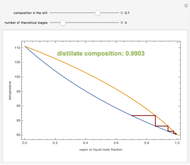
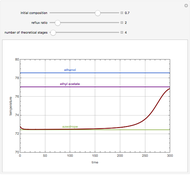
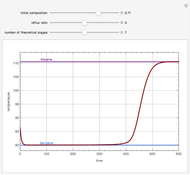
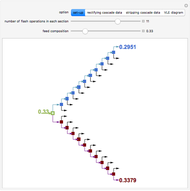
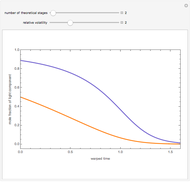
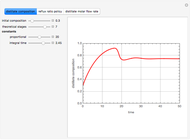
Consider a non-ideal binary mixture composed of acetone and chloroform. This mixture presents a negative azeotrope with a boiling point of 64.48°C and an acetone mole fraction approximately equal to 0.3393.
This Demonstration performs the dynamic simulation of a batch rectification of this mixture. Temperature is plotted versus time for selected values of the initial composition, reflux ratio, and the number of theoretical stages.
The still is charged with 1000 kmol of the initial mixture. The vapor rate is assumed constant at 10 kmol/hr. The molar hold-up of all stages and the condenser are 5 and 20 kmol, respectively.
It is found that (1) the first product to exit the column is a pure component (either chloroform or acetone, depending on the initial composition); (2) if the initial composition is very rich in chloroform (respectively acetone) then this latter component will exit the column first, followed by the binary azeotrope.
If the initial composition is equal to the azeotropic composition, then the temperature remains constant at all times and is equal to the boiling point of the azeotrope.
In addition, the separation is improved if one chooses large reflux ratios or a large number of theoretical stages. Sloppy separation is obtained otherwise.
Browse all topics
