Batting Averages, Weighted Averages, and Simpson's Paradox

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
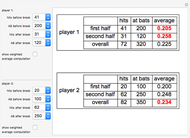
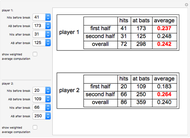
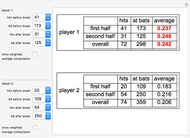
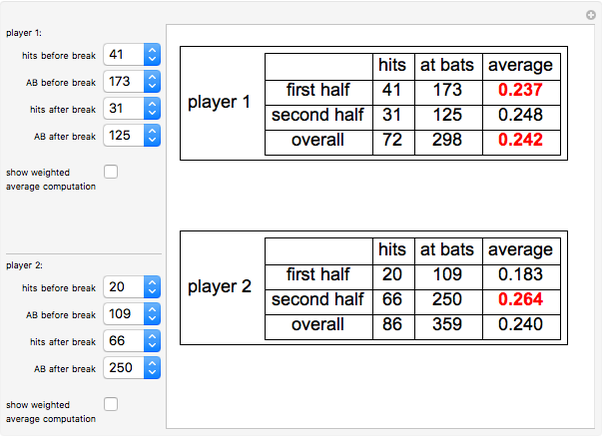
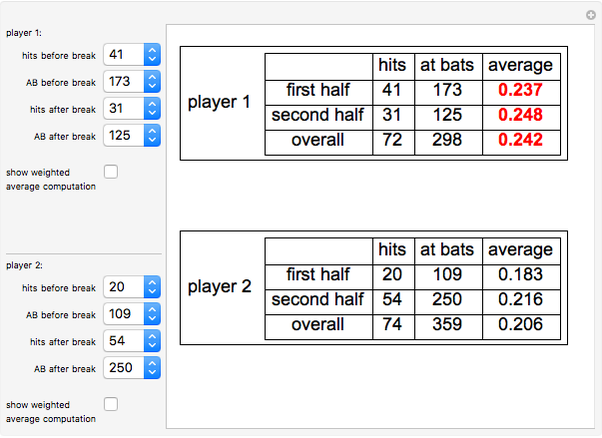
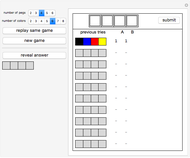
Simpson's paradox refers to the reversal of the direction of an association when a categorical variable is ignored. Although Simpson's paradox can and does occur in such important contexts as death penalty rates and gender equity cases, it is illustrated here in the familiar setting of baseball. It is possible for two baseball players to have a season in which player 1 has a higher batting average than player 2 in the first half of the season and also in the second half of the season, yet player 2 has a higher batting average than player 1 for the entire season. Such a possibility exists because a player's overall batting average for the season is a weighted average of his two half-season averages, weighted by the proportion of at-bats (AB) in each half of the season.
Contributed by: Marc Brodie (Wheeling Jesuit University) (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The operation 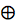 defined by
defined by 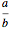
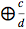 =
= 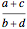 is used to combine the fractions that give a player's half-season batting averages to obtain the overall average. For example, in the thumbnail, player 1's overall average is obtained from the half-season averages by
is used to combine the fractions that give a player's half-season batting averages to obtain the overall average. For example, in the thumbnail, player 1's overall average is obtained from the half-season averages by 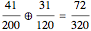 . This operation, in fact, gives a weighted average of the two half-season averages:
. This operation, in fact, gives a weighted average of the two half-season averages: 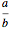
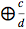 =
=  .
.
Permanent Citation