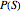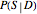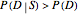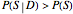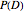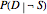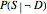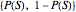Bayes's Theorem and Inverse Probability

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
This Demonstration allows you to explore the quantitative relationship between two conditional probability assessments, 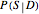 and
and 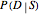 , one the inverse of the other, where
, one the inverse of the other, where 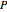 stands for probability,
stands for probability, 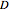 for a proposition about a "diagnostic signal", and
for a proposition about a "diagnostic signal", and 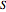 for a proposition about a "state" variable of interest. Typically, the relationship between these inverse probabilities is understood through Bayes's theorem:
for a proposition about a "state" variable of interest. Typically, the relationship between these inverse probabilities is understood through Bayes's theorem:
Contributed by: John Fountain (January 2009)
Open content licensed under CC BY-NC-SA
Snapshots
Details
It is well known (G. Gigerenzer, Calculated Risks: How to Know When Numbers Deceive You, New York: Simon & Schuster, 2002) that many people, including well-educated professionals, do not reason well about uncertainties, especially when that reasoning involves using conditional probabilities. Conceptually, the logical relationships between "signals", such as the outcome of a diagnostic health test, and "states", such as the presence, absence, or severity of a disease, is often misunderstood. Even when the concepts involved are understood, poor quantitative inferences are frequently made, systematically putting too much emphasis on the result of possibly reliable, but imperfect, diagnostic tests, and too little emphasis on the underlying base rates of the state variable. Moreover, there is often a misplaced "illusion of certainty" in whatever quantitative inferences are eventually made: it takes great computational effort to conduct robustness tests unaided (i.e., with pencil and paper) to see whether small changes in assumed or known uncertainties have much of an impact on the final inference that will be used for decision making.
This Demonstration allows you to explore the quantitative relationship between two conditional probability assessments, 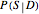 and
and 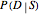 , one the inverse of the other, where
, one the inverse of the other, where 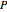 stands for probability,
stands for probability, 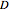 for propositions asserting something about a "diagnostic signal", and
for propositions asserting something about a "diagnostic signal", and 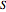 for propositions about some "state" variable of interest, with the symbol
for propositions about some "state" variable of interest, with the symbol 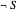 ("not
("not 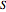 ") indicating the logical negation of the proposition about
") indicating the logical negation of the proposition about 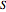 , explained more completely in the next paragraph. Typically the relationship between these inverse probabilities is understood through Bayes's theorem, which can be represented mathematically as a relationship between four probability assessments,
, explained more completely in the next paragraph. Typically the relationship between these inverse probabilities is understood through Bayes's theorem, which can be represented mathematically as a relationship between four probability assessments, 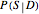 ,
, 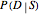 ,
, 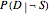 , and
, and 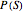 , whereby specifying the last three determines the first, as shown in the following equation:
, whereby specifying the last three determines the first, as shown in the following equation:
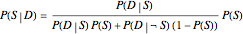 .
.
The controls let you vary separately 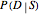 , the sensitivity of the diagnostic test,
, the sensitivity of the diagnostic test, 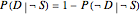 , with
, with 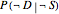 the specificity of the diagnostic test, and
the specificity of the diagnostic test, and 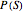 , the base rate of the state variable. The visual output design focuses attention on the effect of these changes in a qualitative and quantitative way on the relationship between the inverse probabilities
, the base rate of the state variable. The visual output design focuses attention on the effect of these changes in a qualitative and quantitative way on the relationship between the inverse probabilities 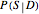 and
and 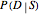 .
.
In a typical interpretation of this symbolism 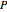 stands for probability, and
stands for probability, and 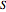 and
and 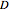 are indicator variables taking on the values 1 or 0 for some observable binary events. Less abstractly we can interpret
are indicator variables taking on the values 1 or 0 for some observable binary events. Less abstractly we can interpret 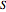 and
and 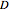 as indicating the truth value of some underlying proposition about observable events (so
as indicating the truth value of some underlying proposition about observable events (so 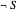 and
and  are propositions that are the corresponding logical negations of the original propositions). For example
are propositions that are the corresponding logical negations of the original propositions). For example 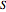 might indicate the truth value of a proposition about someone's health, "Jones has osteoporosis", or someone's educational outcomes, "Smith received a grade of B in the course in 2008", so
might indicate the truth value of a proposition about someone's health, "Jones has osteoporosis", or someone's educational outcomes, "Smith received a grade of B in the course in 2008", so 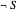 indicates the truth value of the proposition that "Jones does not have osteoporosis" or that "Smith did not receive a grade of B in the course in 2008". Similarly
indicates the truth value of the proposition that "Jones does not have osteoporosis" or that "Smith did not receive a grade of B in the course in 2008". Similarly 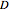 might indicate the truth value of some other underlying proposition about a possibly related observable state of the world. For example
might indicate the truth value of some other underlying proposition about a possibly related observable state of the world. For example 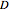 might indicate the truth value of the proposition that "Jones has a bone density measurement two standard deviations below the mean for her age as revealed by a DEXA (dual energy x-ray) scan" or that "Smith attended more than half of the tutorials for the course in 2008", with
might indicate the truth value of the proposition that "Jones has a bone density measurement two standard deviations below the mean for her age as revealed by a DEXA (dual energy x-ray) scan" or that "Smith attended more than half of the tutorials for the course in 2008", with  the negation of the relevant proposition.
the negation of the relevant proposition.
Logically, there are four possibilities for the values of the indicator variables 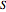 and
and 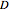 considered jointly,
considered jointly,  ,
, 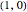 ,
, 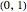 ,
, 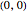 . Uncertainty about the variables
. Uncertainty about the variables 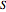 and
and 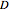 may be expressed as a coherent, discrete, joint probability distribution
may be expressed as a coherent, discrete, joint probability distribution 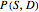 over this four-element set, specifying four elementary probabilities on the space of logically possible joint outcomes
over this four-element set, specifying four elementary probabilities on the space of logically possible joint outcomes  :
: 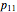 ,
, 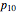 ,
,  ,
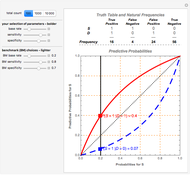
, 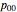 , with obvious notation. Of course, since these probabilities have to add up to 1, there are really only three independent numbers that will completely tie down this joint probability distribution. But specifying three numbers for a joint probability distribution is not the only way of thinking about one's uncertainty about several variables and their possible and probable interrelationships. Nor is it the way used in practice by many of the professional decision makers studied in Gigerenzer's research. This is not surprising when information relevant to calibrating and assessing one's uncertainty is partial and incomplete.
, with obvious notation. Of course, since these probabilities have to add up to 1, there are really only three independent numbers that will completely tie down this joint probability distribution. But specifying three numbers for a joint probability distribution is not the only way of thinking about one's uncertainty about several variables and their possible and probable interrelationships. Nor is it the way used in practice by many of the professional decision makers studied in Gigerenzer's research. This is not surprising when information relevant to calibrating and assessing one's uncertainty is partial and incomplete.
How else might one proceed? For definiteness, take the health example where 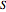 is the truth value of the proposition "Jones has osteoporosis" and
is the truth value of the proposition "Jones has osteoporosis" and 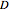 is the truth value of the proposition "Jones has a bone density measurement two standard deviations below the mean for her age as revealed by a DEXA (dual energy x-ray) scan". One might have very good information on the prevalence of the disease, helping to tie down
is the truth value of the proposition "Jones has a bone density measurement two standard deviations below the mean for her age as revealed by a DEXA (dual energy x-ray) scan". One might have very good information on the prevalence of the disease, helping to tie down 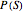 , commonly known as the base rate of the state. Perhaps also there is some limited information on diagnostic test results from those who definitely have osteoporosis, providing information for an assessment of
, commonly known as the base rate of the state. Perhaps also there is some limited information on diagnostic test results from those who definitely have osteoporosis, providing information for an assessment of 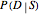 and
and 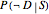 , where
, where 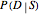 is commonly known as the sensitivity of the diagnostic test: given that Jones has the disease, how likely is it that the test will pick that up and show a positive result? Likewise, other available information sources might help tie down the chances of positive or negative diagnostic test results for those who do not have osteoporosis,
is commonly known as the sensitivity of the diagnostic test: given that Jones has the disease, how likely is it that the test will pick that up and show a positive result? Likewise, other available information sources might help tie down the chances of positive or negative diagnostic test results for those who do not have osteoporosis, 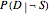 and
and 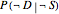 , with
, with 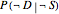 commonly known as the specificity of the diagnostic test: given that Jones doesn't have the disease, how likely is it that the test will pick that up and show a negative result? Alternatively, one might have information on the true or false positive rates,
commonly known as the specificity of the diagnostic test: given that Jones doesn't have the disease, how likely is it that the test will pick that up and show a negative result? Alternatively, one might have information on the true or false positive rates, 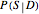 or
or 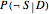 , and true or false negative rates,
, and true or false negative rates, 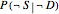 or
or 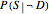 , conditional on outcomes of the diagnostic test, or information on the marginal chances
, conditional on outcomes of the diagnostic test, or information on the marginal chances 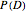 of having a positive test result for osteoporosis. With this multiplicity of important but complex ways of thinking about uncertainty about
of having a positive test result for osteoporosis. With this multiplicity of important but complex ways of thinking about uncertainty about  it is no wonder that Gigerenzer finds even well-educated people becoming confused when they try to reason under uncertainty.
it is no wonder that Gigerenzer finds even well-educated people becoming confused when they try to reason under uncertainty.
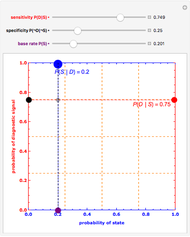
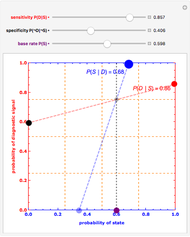
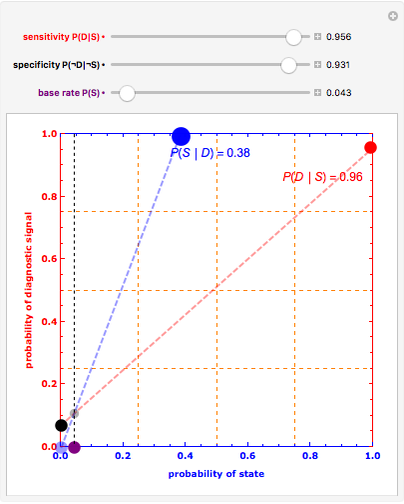
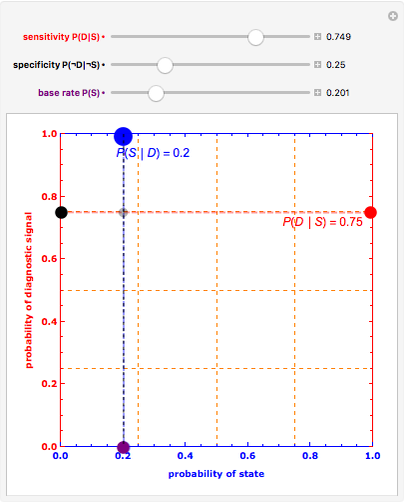
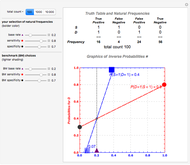
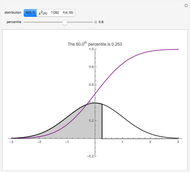
The red and blue dotted lines in the animation are helpful in visualizing the constraints involved in making inferences. The red dotted line between the conditional probabilities 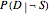 and
and 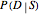 traces out the marginal probability
traces out the marginal probability 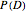 , a weighted average of the two endpoint conditionals using the base rate
, a weighted average of the two endpoint conditionals using the base rate 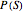 to specify a weighting function. Similarly, the blue dotted line between
to specify a weighting function. Similarly, the blue dotted line between 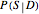 and
and 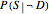 traces out the marginal probability
traces out the marginal probability 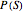 , a weighted average of the two endpoint conditionals using
, a weighted average of the two endpoint conditionals using 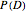 to specify a weighting function. A specification of either the three uncertainties
to specify a weighting function. A specification of either the three uncertainties  or the three uncertainties
or the three uncertainties 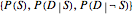 fully determines the joint probability distribution
fully determines the joint probability distribution 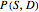 . The Demonstration and the logic that is usually followed in applying Bayes's theorem specify
. The Demonstration and the logic that is usually followed in applying Bayes's theorem specify 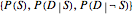 , so that the other triple of probabilities
, so that the other triple of probabilities 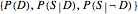 is fully determined. Anyone curious about what happens if less than three separate pieces of information are used to try to assess uncertainty about signals and states, and the effect those incomplete specifications of uncertainties can have on inverse inference, should have a look at Chapter 3 of F. Lad's Operational Subjective Statistical Methods: A Mathematical, Philosophical, and Historical Introduction, New York: Wiley, 1996. Indeed the geometric reasoning that led to this Demonstration was inspired by the many beautiful, albeit static, 2D and 3D images in Lad's book.
is fully determined. Anyone curious about what happens if less than three separate pieces of information are used to try to assess uncertainty about signals and states, and the effect those incomplete specifications of uncertainties can have on inverse inference, should have a look at Chapter 3 of F. Lad's Operational Subjective Statistical Methods: A Mathematical, Philosophical, and Historical Introduction, New York: Wiley, 1996. Indeed the geometric reasoning that led to this Demonstration was inspired by the many beautiful, albeit static, 2D and 3D images in Lad's book.
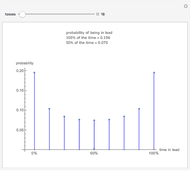
As noted above, Gigerenzer's research shows that well-educated people typically, and easily, become confused about the logical relationships between the many different notions of probability, even when there are only two simple, binary discrete variables involved (signal and state). But confusion does not necessarily lead to a decision-making crisis. It can be an opportunity to learn. Indeed, I have had great success in teaching undergraduate students in game theory about inverse probability using a static version of this Demonstration in conjunction with logical truth tables and Gigerenzer's "natural frequency" language for reasoning with conditional probabilities. Note: these students typically span the spectrum of social and physical sciences and humanities with most having no prior statistical training whatsoever, and yet, by the end of the course, over 80% appear to both understand the ideas involved in Bayes's theorem and inverse probability and are able to accurately solve simple inverse probability problems using these geometric methods. The freely accessible video clips of my Introductory Game Theory courseshow how these ideas are implemented.
Snapshot 1: a diagnostic test that is very good at ruling out negative states and detecting positive states, both sensitivity and specificity at 93%, still gives only a moderate inverse inference (36%) from a positive test result when the original base rate is low (4%)
Snapshot 2: a completely uninformative test
Snapshot 3: a diagnostic test that is good at ruling out negative states but only just better than chance at detecting positive states, yielding a large improvement in predictive probability from a positive test result
Permanent Citation