Bicycle or Unicycle Tracks?

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
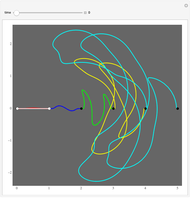
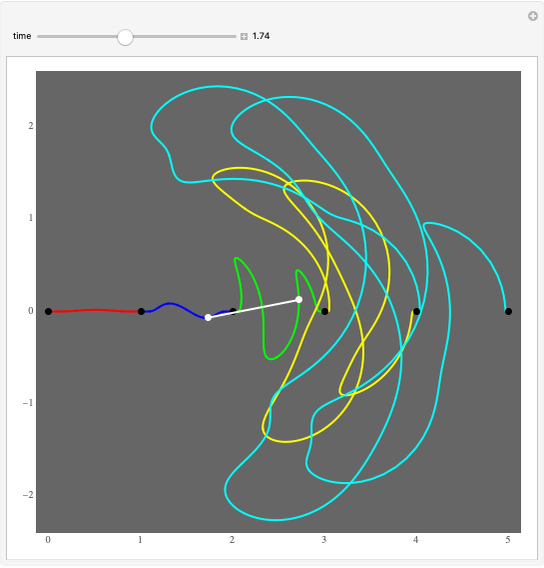
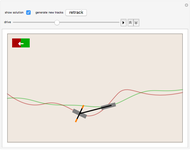
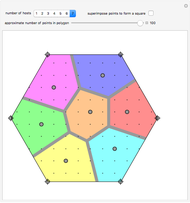
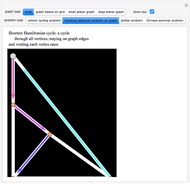
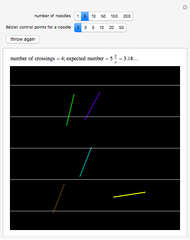
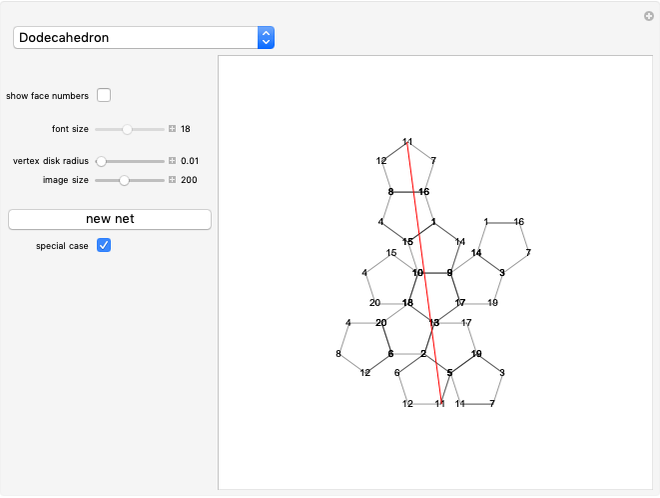
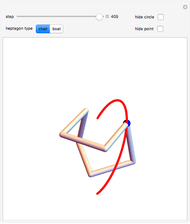
The two wheels of a bicycle typically make separate tracks. One exception is a bike traveling in a straight line. The convoluted path shown in the graphic is an example of a nonstraight track along which a bike travels so that the rear wheel follows exactly in the track made by the front wheel. If  is the parametrized curve, then
is the parametrized curve, then 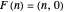 , and the white unit tangent vector at
, and the white unit tangent vector at 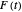 ends at
ends at 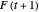 . This vector represents the bicycle.
. This vector represents the bicycle.
Contributed by: Stan Wagon (December 2017)
(Macalester College)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The curve is defined by starting with the red path and then extending rightward by adding the unit tangent vector. This construction yields an ambiguous bicycle-unicycle path for all 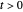 . The initial curve from
. The initial curve from 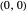 to
to 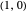 that gets the process started is the singular function
that gets the process started is the singular function 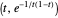 , which shows a single small bump. Snapshot 1 shows how that single bump becomes a double bump in the next segment. All derivatives of this function at
, which shows a single small bump. Snapshot 1 shows how that single bump becomes a double bump in the next segment. All derivatives of this function at  or
or  are
are 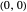 , except the first derivative, which is
, except the first derivative, which is 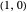 . This property is preserved at the end points of all the other unit-time-interval segments going forward. This construction is due to David Finn [1].
. This property is preserved at the end points of all the other unit-time-interval segments going forward. This construction is due to David Finn [1].
Reference
[1] D. Finn, "Can a Bicycle Create a Unicycle Track?," The College Mathematics Journal, 33(4), 2002 pp. 283–292. doi:10.2307/1559048.
Permanent Citation