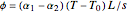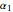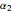Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Bimetallic Spiral Thermometer

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

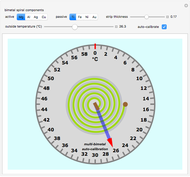
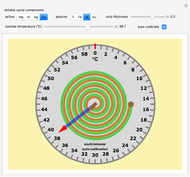
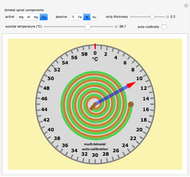
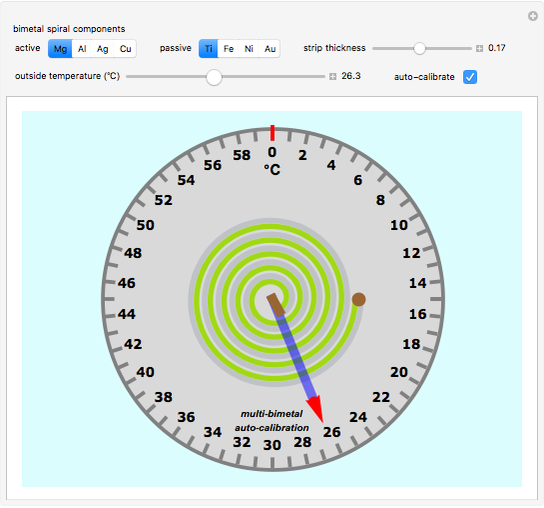
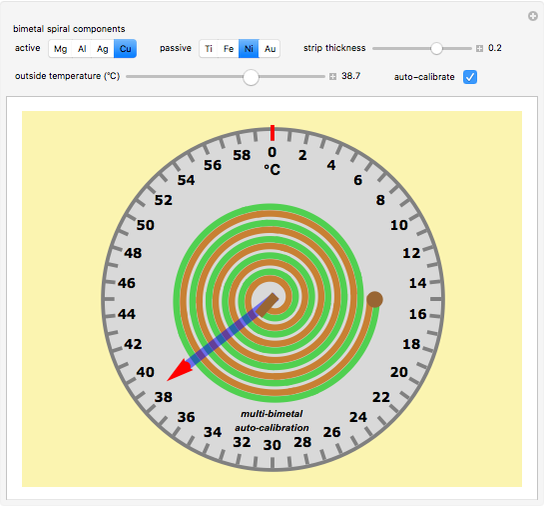
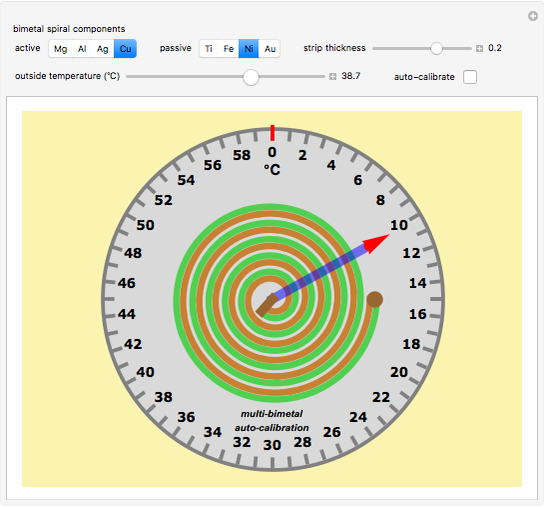
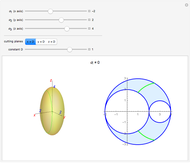
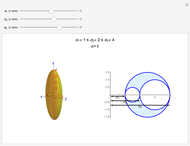
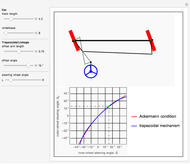
This Demonstration simulates a classical bimetallic spiral thermometer (dial or coil thermometer).

[more]

An Archimedes's spiral made of a coiled bimetal strip gives a deflection proportional to the surrounding temperature and can serve as a thermometer.

The angular deflection of a bimetal spiral of length and strip thickness is given by , where and are the coefficients of linear expansion of the component materials used.

[less]

Contributed by: Erik Mahieu (December 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

For the arc length of Archimedes's spiral, we use the classical formula (Wolfram|Alpha)

,

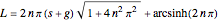where is the gap.

The thermometer is by default calibrated for the Mg/Fe bimetal. Other bimetal settings need to be calibrated individually. To do this, we insert a linear factor cal60, computed with Mathematica's built-in function FindRoot, to give a deflection of 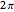at 60 °C.

Snapshot 1: a very sensitive bimetal Mg/Ti with thermal expansion coefficients of 26/8.6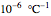

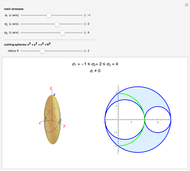
Snapshot 2: a less sensitive bimetal Cu/Ni with thermal expansion coefficients of 17/13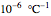

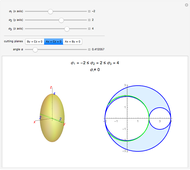
Snapshot 3: the uncalibrated version of Snapshot 2

For extensive information about bimetals, see "Thermostatic Bimetal Handbook" from Kanthal AB, Sweden.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send