Bimodal Size Distributions in Grinding and Attrition

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
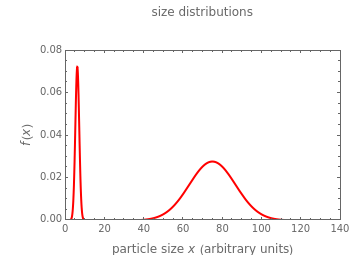
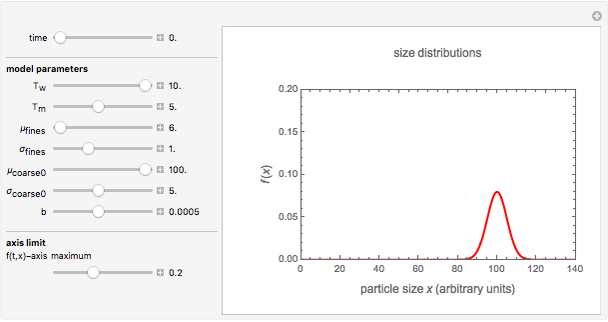
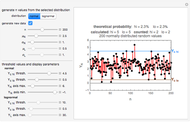
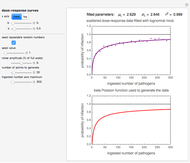
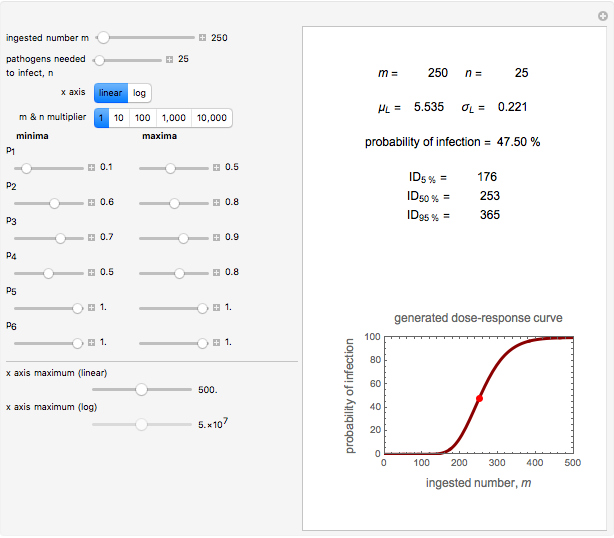
This Demonstration simulates the varying particle size distributions during the disintegration of particulates. It enables visualization of the difference when either particle shattering or surface attrition dominates the disintegration process or when the two play a comparable role. The actual scenario is determined by the relative time scale of the size reduction of the coarse fraction and that of the fines formation. The Demonstration is based on both fractions having normal size distributions and hence not all plots generated by the Demonstration correspond to real-life particulates.
Contributed by: Mark D. Normand and Micha Peleg (August 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Snapshot 1: initial particle size distribution
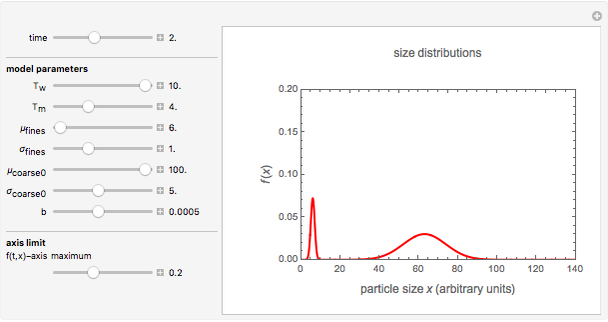
Snapshot 2: dominant shattering of the coarse fraction, after time = 2 (arbitrary units)
Snapshot 3: dominant erosion of the coarse fraction, after time = 2 (arbitrary units)
Snapshot 4: shattering and erosion playing a comparable role, after time = 2 (arbitrary units)
This Demonstration simulates the evolution of the size distribution of particulates undergoing grinding or attrition. It starts with a coarse fraction whose normal size distribution's parameters are  and
and  . As the process progresses, the coarse fraction's mean,
. As the process progresses, the coarse fraction's mean,  , and standard deviation,
, and standard deviation,  , vary in a manner controlled by a characteristic time,
, vary in a manner controlled by a characteristic time,  , and a span parameter,
, and a span parameter,  . At the same time, a fines fraction, which has a constant size distribution characterized by
. At the same time, a fines fraction, which has a constant size distribution characterized by 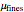 and
and 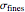 , is formed. The rate of its formation, in terms of its mass fraction, is controlled by a characteristic time,
, is formed. The rate of its formation, in terms of its mass fraction, is controlled by a characteristic time,  .
.
The instantaneous weight fraction of the fines is calculated using 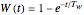 .
.
During the process, the momentary coarse fraction's mean and standard deviation are calculated with the equations 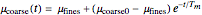 and
and  , respectively.
, respectively.
The time,  , and all model parameters,
, and all model parameters,  ,
,  ,
, 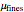 ,
, 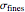 ,
,  ,
, 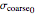 , and
, and  are in arbitrary units and are entered with sliders.
are in arbitrary units and are entered with sliders.
The upper limit of the  axis is also entered with a slider.
axis is also entered with a slider.
Reference
[1] L. M. Popplewell, O. H. Campanella, and M. Peleg, "Simulation of Bimodal Size Distributions in Aggregation and Disintegration Processes," Chemical Engineering Progress, 85, 1989 pp. 56–62.
Permanent Citation