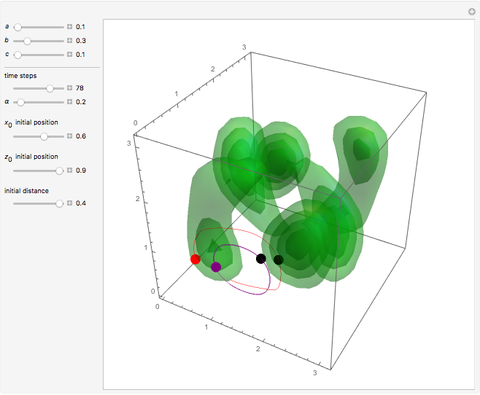
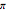Bohm Trajectories for a Particle in an Infinite 3D Box

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
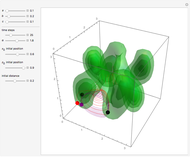
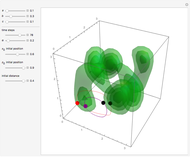
Quantum motion occurs in configuration-space particle trajectories associated with the de Broglie–Bohm causal interpretation of quantum mechanics. Previous Demonstrations (see related links) showed that the motion of a quantum particle could be obtained when the corresponding particle density (given by the modulus of the Schrödinger wavefunction) is not time dependent. In addition to [1], the conditions for chaotic behavior can occur in a system with three degrees of freedom for a time independent wavefunction.
[more]
Contributed by: Klaus von Bloh (August 2013)
Open content licensed under CC BY-NC-SA
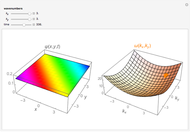
Snapshots
Details
A degenerate, unnormalized wavefunction for the three-dimensional box can be expressed by  , where
, where 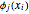 and
and 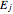 are eigenfunctions and permuted eigenenergies of the corresponding stationary one-dimensional Schrödinger equation with
are eigenfunctions and permuted eigenenergies of the corresponding stationary one-dimensional Schrödinger equation with 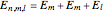 . By expressing the wavefunction
. By expressing the wavefunction 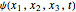 in the eikonal form
in the eikonal form 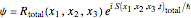 , the particle density and the velocity for this special superposition state become time independent.
, the particle density and the velocity for this special superposition state become time independent.
In the case of the three-dimensional box, the eigenfunctions and eigenenergies that obey the free stationary Schrödinger equation with Dirichlet boundary condition are: 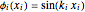 , with the wavenumbers
, with the wavenumbers 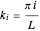 , and the total energy
, and the total energy  , where
, where  ,
,  ,
, 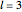 , and
, and  . Adopting
. Adopting 
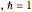 , and
, and  , the equations turn into the desired form. The corresponding autonomous differential equation system (velocity field) is derived from the phase function of the total wavefunction.
, the equations turn into the desired form. The corresponding autonomous differential equation system (velocity field) is derived from the phase function of the total wavefunction.
In the program, increase PlotPoints, AccuracyGoal, PrecisionGoal, and MaxSteps for greater accuracy.
Reference
[1] R. H. Parmenter and R. W. Valentine, "Deterministic Chaos and the Causal Interpretation of Quantum Mechanics," Physics Letters A, 201, 1995 pp. 1–8. doi:10.1016/0375-9601(96)00096-5.
Permanent Citation