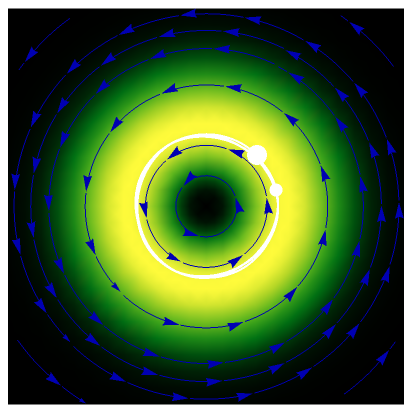
Bohm Trajectories for an Isotropic Harmonic Oscillator with Added Inverse Quadratic Potential

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
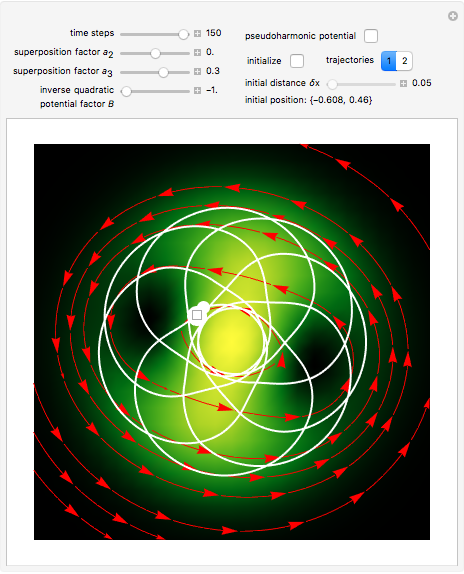
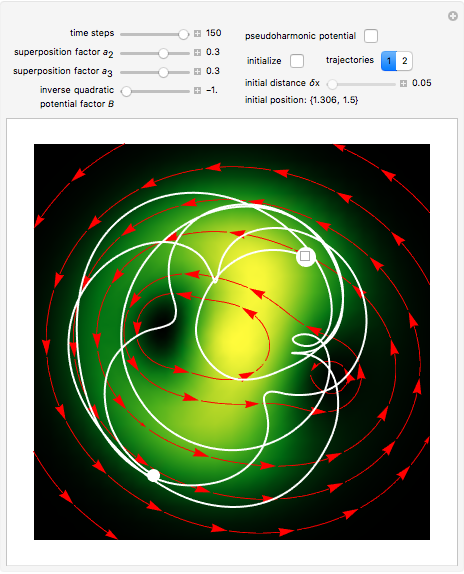
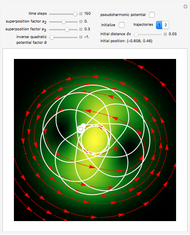
This Demonstration considers two-dimensional Bohm trajectories in a central field represented by an isotropic harmonic oscillator augmented by an inverse quadratic potential plus a constant 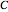 . This is called a pseudoharmonic-type potential, with the form
. This is called a pseudoharmonic-type potential, with the form  . Exact solutions of the Schrödinger equation for this potential are known. An analogous potential in three dimensions can represent the interaction of some diatomic molecules [1]. Obviously, the pseudoharmonic oscillator behaves asymptotically as a harmonic oscillator, but has a singularity at
. Exact solutions of the Schrödinger equation for this potential are known. An analogous potential in three dimensions can represent the interaction of some diatomic molecules [1]. Obviously, the pseudoharmonic oscillator behaves asymptotically as a harmonic oscillator, but has a singularity at  For
For 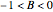 , there is a small region where the potential exhibits a repulsive inverse-square-type character. Possible trajectories can then exhibit a rich dynamical structure, depending on the parameters
, there is a small region where the potential exhibits a repulsive inverse-square-type character. Possible trajectories can then exhibit a rich dynamical structure, depending on the parameters 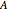 ,
, 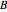 of the potential and the initial starting points. The motion ranges from periodic to quasi-periodic to fully chaotic. In the de Broglie–Bohm (or causal) interpretation of quantum mechanics [2, 3], the particle position and momentum are well defined, and the motion can be described by continuous evolution according to the time-dependent Schrödinger equation. In contrast to [4], the conditions for chaotic behavior can occur in a system with two degrees of freedom and for a superposition of two stationary states. See, for example,
of the potential and the initial starting points. The motion ranges from periodic to quasi-periodic to fully chaotic. In the de Broglie–Bohm (or causal) interpretation of quantum mechanics [2, 3], the particle position and momentum are well defined, and the motion can be described by continuous evolution according to the time-dependent Schrödinger equation. In contrast to [4], the conditions for chaotic behavior can occur in a system with two degrees of freedom and for a superposition of two stationary states. See, for example, 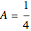 ,
, 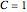 (in the
(in the 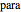 variable in the program),
variable in the program),  ,
, 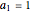 ,
, 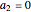 ,
, 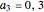 and the initial position
and the initial position 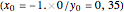 , two trajectories with initial distance
, two trajectories with initial distance 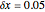 .
.
Contributed by: Klaus von Bloh (October 2018)
Open content licensed under CC BY-NC-SA
Details
The two-dimensional stationary Schrödinger equation with potential 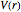 , a function
only of the distance
, a function
only of the distance  from the origin, can be written:
from the origin, can be written:
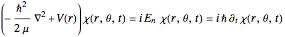
with the potential
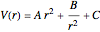 ,
,
reduced mass  , Planck's constant
, Planck's constant  , the constants
, the constants 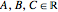 and the Laplacian operator
and the Laplacian operator 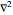 in plane polar coordinates. For simplicity, set
in plane polar coordinates. For simplicity, set  and
and  equal to 1. The solution of the Schrödinger equation for the quantum system with the pseudoharmonic-type potential gives to the eigenfunction
equal to 1. The solution of the Schrödinger equation for the quantum system with the pseudoharmonic-type potential gives to the eigenfunction 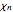 (for detailed information, see [5]) in plane polar coordinates:
(for detailed information, see [5]) in plane polar coordinates:
with 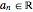 , the integer
, the integer  and with the eigenenergy
and with the eigenenergy 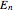 :
:
In Cartesian coordinates (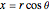 ,
, 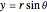 ), the solution reads:
), the solution reads:
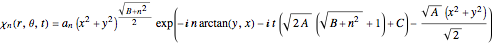 .
.
or in Cartesian coordinates:
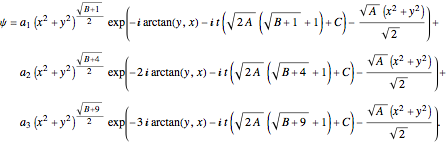
For 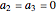 , the velocity field becomes autonomous and obeys the time-independent part of the continuity equation
, the velocity field becomes autonomous and obeys the time-independent part of the continuity equation
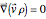
with  ; the trajectories reduce to circles with the velocities
; the trajectories reduce to circles with the velocities  and
and 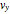 :
:
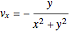 and
and  .
.
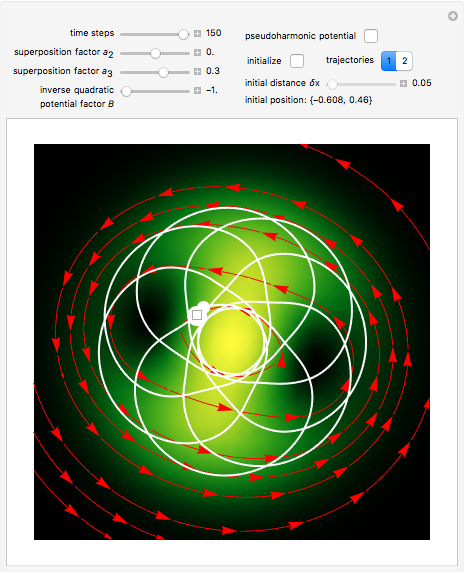
When PlotPoints, AccuracyGoal, PrecisionGoal and MaxSteps are increased (if enabled), the results will be more accurate. The initial distance between the two starting trajectories is determined by the factor 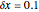 . In the program, you can change the parameters of the potential.
. In the program, you can change the parameters of the potential.
References
[1] K. J. Oyewumi and K. D. Sen,"Exact Solutions of the Schrödinger Equation for the Pseudoharmonic Potential: An Application to Some Diatomic Molecules," Journal of Mathematical Chemistry, 50(5), 2012 pp. 1039–1059. doi:10.1007/s10910-011-9967-4.
[2] Bohmian-Mechanics.net. (Oct 8, 2018) www.mathematik.uni-muenchen.de/~bohmmech/BohmHome/index.html.
[3] S. Goldstein, "Bohmian Mechanics." The Stanford Encyclopedia of Philosophy (Summer 2017 Edition). (Oct 2, 2018)plato.stanford.edu/entries/qm-bohm.
[4] R. H. Parmenter and R. W. Valentine, "Deterministic Chaos and the Causal Interpretation of Quantum Mechanics," Physics Letters A, 201(1), 1995 pp. 1–8. doi:10.1016/0375-9601(95)00190-E.
[5] S. M. Ikhdair and R. Sever, "Exact Solutions of the Radial Schrödinger Equation for Some Physical Potentials," Central European Journal of Physics, 5(4), 2007 pp. 516–527. doi:10.2478/s11534-007-0022-9.
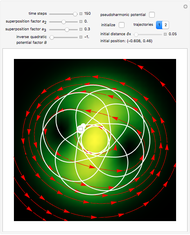
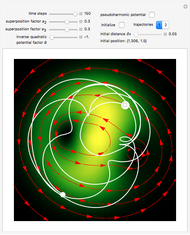
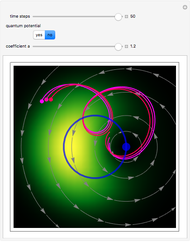
Snapshots
Permanent Citation