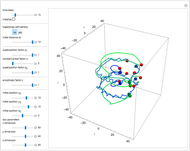
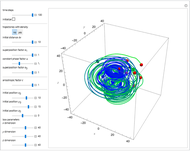
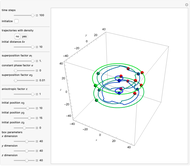
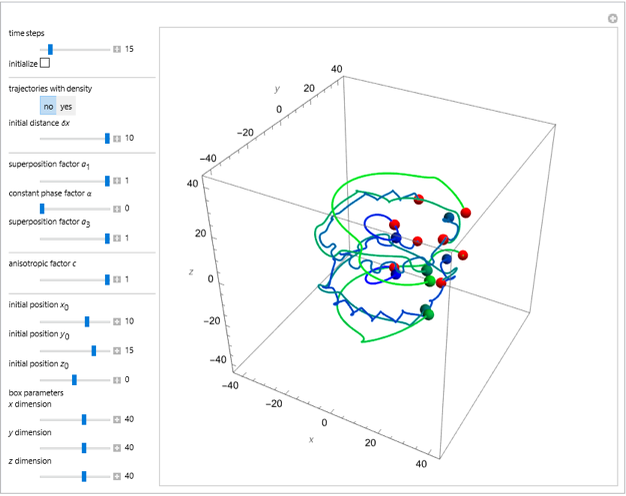
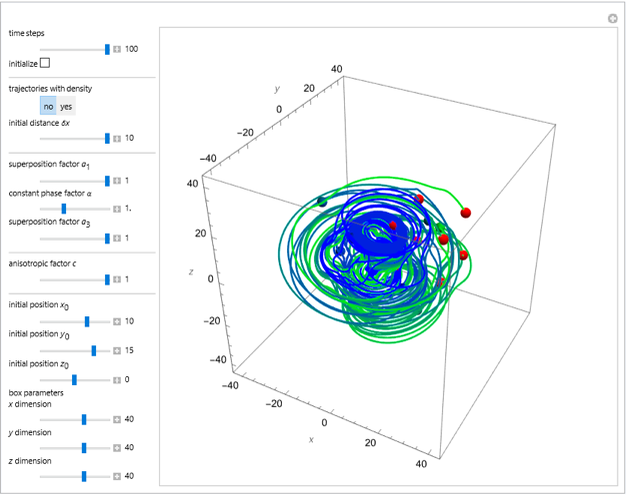
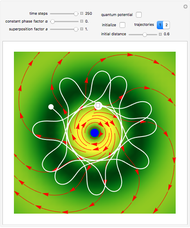
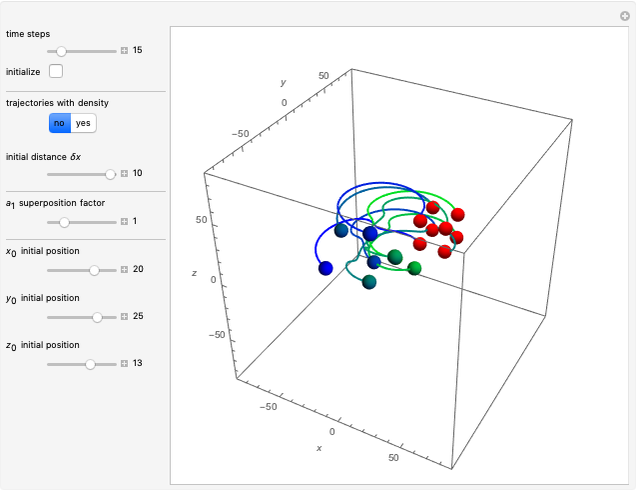
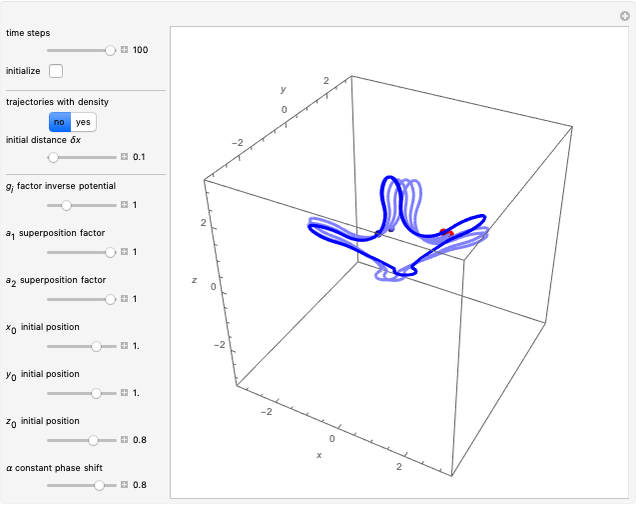
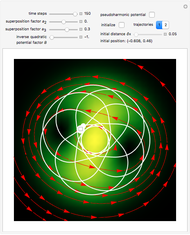
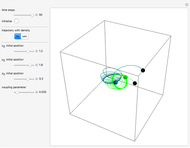
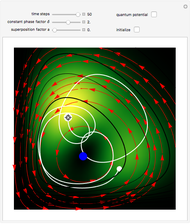
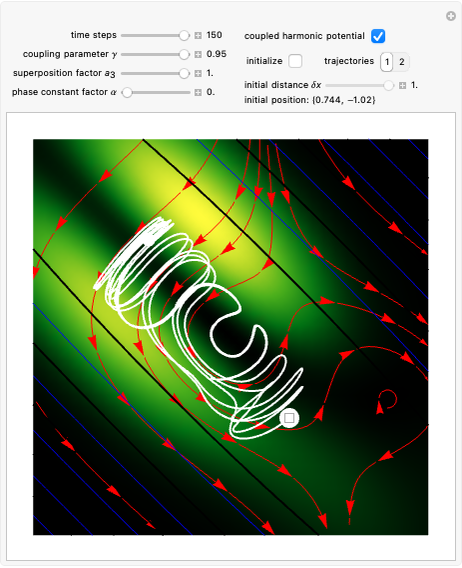
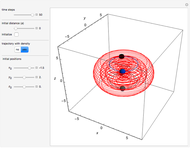
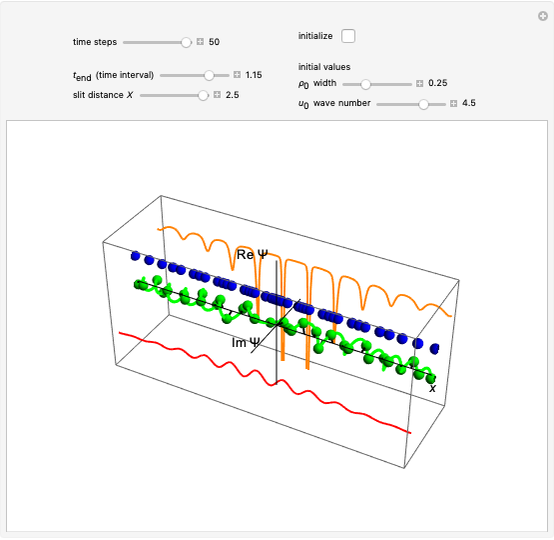
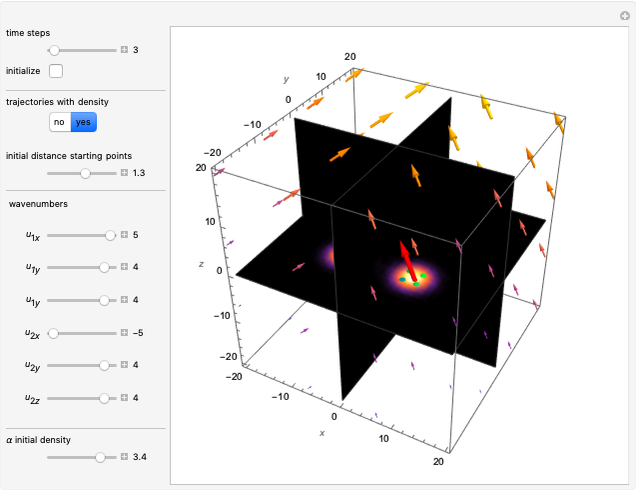
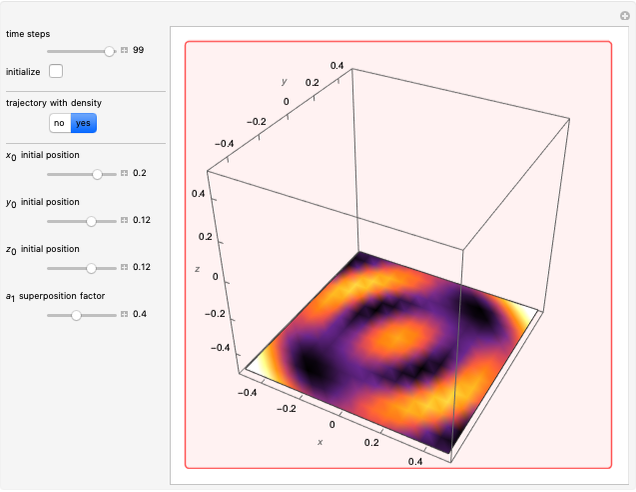
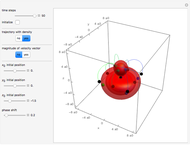
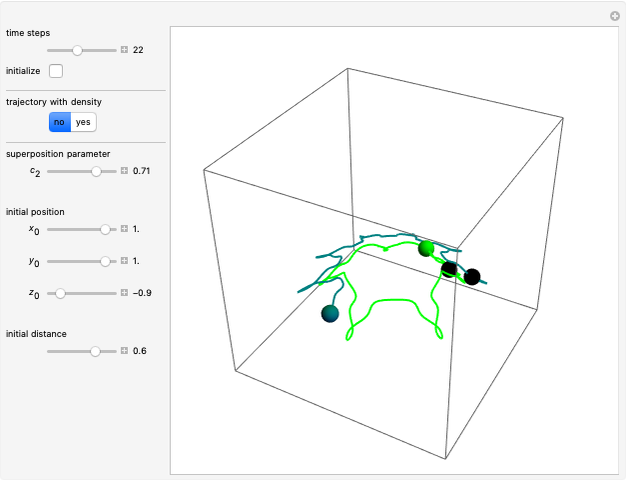
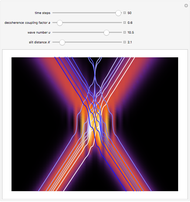
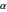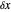Bohm Trajectories for the Anisotropic Coulomb Potential with Constant Phase Shift

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
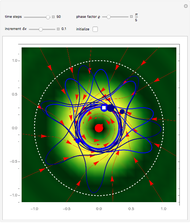
In the nonrelativistic de Broglie–Bohm approach, the electron in a hydrogen-like atom is not moving in the stationary  state. More generally, this is true when the phase function does not depend on the spatial coordinates or when the wavefunction is a real-valued function. For the hydrogen-like atom in an eigenstate, the electron can be considered to be in motion if the magnetic quantum number
state. More generally, this is true when the phase function does not depend on the spatial coordinates or when the wavefunction is a real-valued function. For the hydrogen-like atom in an eigenstate, the electron can be considered to be in motion if the magnetic quantum number 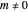 . The quantum particle orbits the
. The quantum particle orbits the  axis in a circle of constant radius
axis in a circle of constant radius  (for more details see [1]). In most other cases, any superposition state leads to a moving electron.
(for more details see [1]). In most other cases, any superposition state leads to a moving electron.
Contributed by: Klaus von Bloh (June 13)
Open content licensed under CC BY-NC-SA
Details
The three-dimensional stationary Schrödinger equation with Coulomb potential 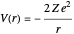 can be written in parabolic coordinates
can be written in parabolic coordinates 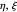 as
as
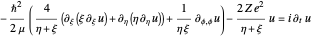 ,
,
with the wavefunction  , the Laplace operator
, the Laplace operator 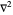 , the partial derivative
, the partial derivative 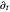 with respect to time and the Coulomb potential
with respect to time and the Coulomb potential 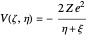 . For simplicity, we set atomic units
. For simplicity, we set atomic units 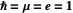 .
.
In spherical polar coordinates, the unnormalized energy eigenfunctions for the hydrogen atom associated with the quantum state with the quantum numbers 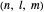 is given by:
is given by:
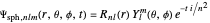 ,
,
where 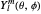 is a spherical harmonic. The radial function is
is a spherical harmonic. The radial function is
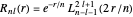 ,
,
where 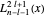 is a generalized Laguerre polynomial.
is a generalized Laguerre polynomial.
For a stationary case with 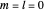 , the phase function
, the phase function 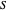 reduces to zero. Thus the Bohm momentum
reduces to zero. Thus the Bohm momentum 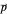 of the ground state electron is
of the ground state electron is 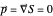 , and finally the electron is at rest [1]. For
, and finally the electron is at rest [1]. For 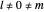 , the electron is in motion.
, the electron is in motion.
If the wavefunction is expressed in parabolic coordinates (for more details see [4–6]), we find:
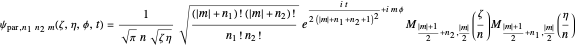 ,
,
where
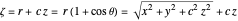 ,
,
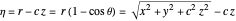 ,
,
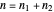 .
.
Here 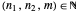 ,
, 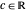 and
and 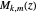 is a Whittaker function.
is a Whittaker function.
The energy spectrum depends only on the integers 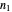 ,
, 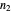 and
and 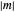 .
.
For the anisotropic Coulomb potential, the Schrödinger equation in Cartesian coordinates is:
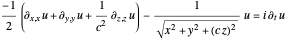
with
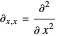 ,
,
and so on.
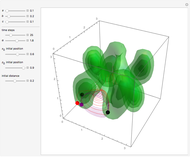
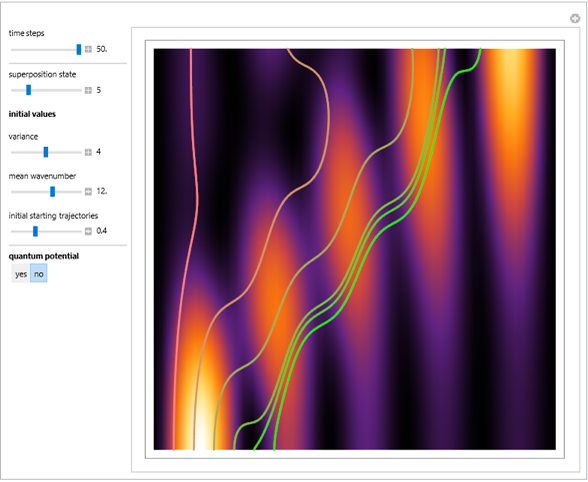
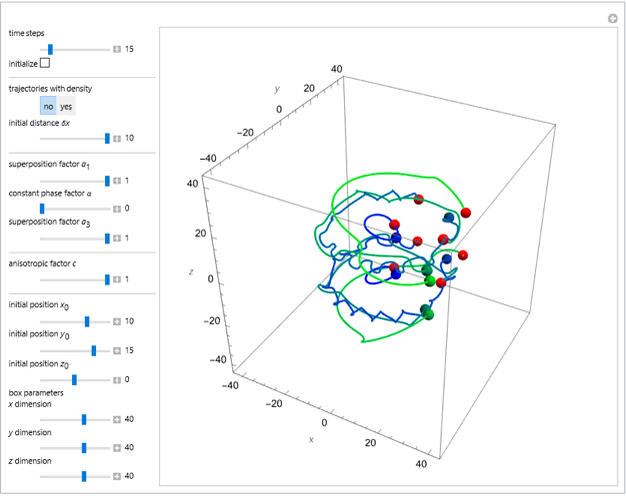
Due to computational limitations, the superposed total wavefunctions 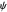 are taken as a sum of just three eigenfunctions
are taken as a sum of just three eigenfunctions 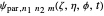 , where the unnormalized wavefunction
, where the unnormalized wavefunction 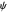 for a particle is written as:
for a particle is written as:
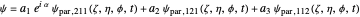 ,
,
with 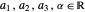 and (here,
and (here, 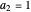 ).
).
Each part of the superposition of the three stationary state has the same energy:
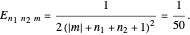
The parabolic wavefunction 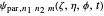 could be expressed by a linear combination of stationary states of spherical wavefunction
could be expressed by a linear combination of stationary states of spherical wavefunction 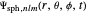 . For example,
. For example,
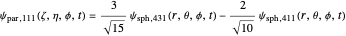 .
.
Let 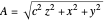 for convenience. After variable transformations from parabolic coordinates to Cartesian coordinates, we obtain the total phase function
for convenience. After variable transformations from parabolic coordinates to Cartesian coordinates, we obtain the total phase function  :
:
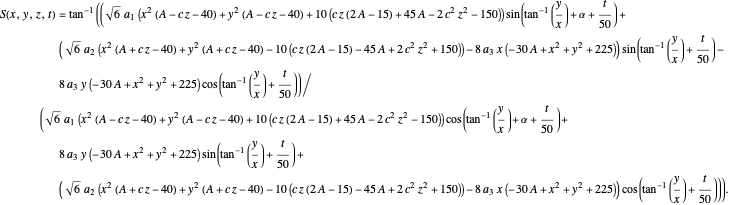
The gradient of the phase 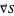 is obtained from the total wavefunction in polar form,
is obtained from the total wavefunction in polar form, 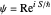 , with the quantum amplitude
, with the quantum amplitude 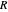 . The velocity field
. The velocity field 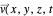 is calculated by the Bohm momentum
is calculated by the Bohm momentum 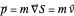 with mass
with mass 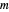 . From the Bohm momentum
. From the Bohm momentum 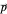 it follows that
it follows that
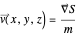
(here, 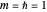 ).
).
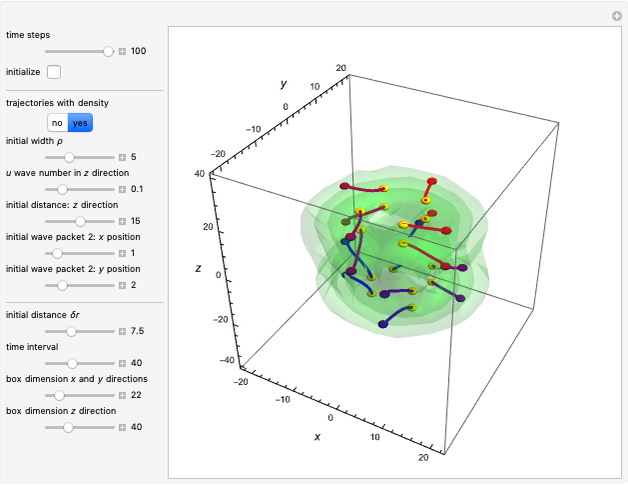
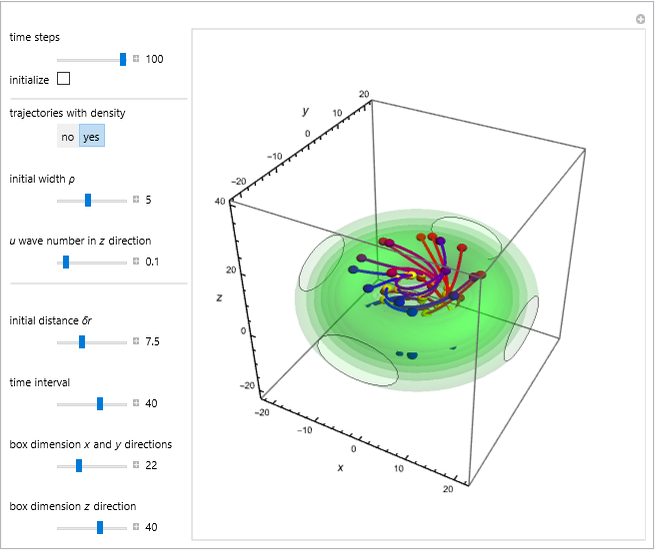
In the case of the superposition of the three stationary states with equal energy, the corresponding differential equation system for the velocity field becomes autonomous and obeys the time-independent part of the continuity equation 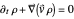 with the wave density
with the wave density 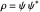 .
.
For 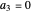 the wavefunction
the wavefunction 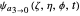 in parabolic coordinates reduces to
in parabolic coordinates reduces to 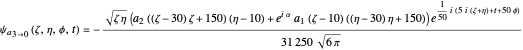 ,
,
with the total phase function 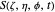 :
:
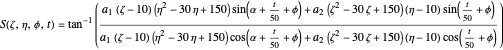 .
.
This could be simplified for 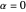 :
:
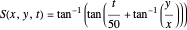 .
.
The trajectories reduce to circles with the velocities:
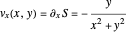 ,
,
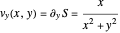
and
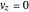 .
.
The velocity depends on the position of the particle only. For 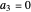 and
and 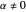 , most of the orbits form "spirally circles" along the
, most of the orbits form "spirally circles" along the  axis, in which a spiral orbit is perpendicular on the circle orbit (for an example, see [7]).
axis, in which a spiral orbit is perpendicular on the circle orbit (for an example, see [7]).
In all other cases, the integration of the velocity vector  in respect to time leads to complex periodic or chaotic orbits (for examples, see [8, 9]). If
in respect to time leads to complex periodic or chaotic orbits (for examples, see [8, 9]). If 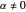 with
with 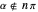 (
(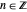 ), it is strongly implied that chaotic motion occurs.
), it is strongly implied that chaotic motion occurs.
 When PlotPoints, AccuracyGoal, PrecisionGoal and MaxSteps are increased (if enabled), the results will be more accurate.
When PlotPoints, AccuracyGoal, PrecisionGoal and MaxSteps are increased (if enabled), the results will be more accurate.
References
[1] P. R. Holland, The Quantum Theory of Motion: An Account of the de Broglie–Bohm Causal Interpretation of Quantum Mechanics, New York: Cambridge University Press, 1993.
[2] Bohmian-Mechanics.net. (Dec 26, 2022) bohmian-mechanics.net.
[3] S. Goldstein, "Bohmian Mechanics." The Stanford Encyclopedia of Philosophy (Summer 2017 Edition). (Dec 26, 2022) plato.stanford.edu/entries/qm-bohm.
[4] L. I. Schiff, Quantum Mechanics, 2nd ed., New York: McGraw-Hill, 1955.
[5] E. Merzbacher, Quantum Mechanics, New York: Wiley, 1961.
[6] J. F. Ogilvie, "The Hydrogen Atom According to Wave Mechanics: Part II. Paraboloidal Coordinates," Revista de Ciencia y Tecnologia, 32(2), 2016 pp. 25–39. arXiv:1612.05098.
[7] K. von Bloh. Bohm Trajectories for the Anisotropic Coulomb Potential with Constant Phase Shift: Part 3 [Video]. (Dec 28, 2022) www.youtube.com/watch?v=kIxbf256IlE.
[8] K. von Bloh. Bohm Trajectories for the Anisotropic Coulomb Potential in Parabolic Coordinates: Part 1 [Video]. (Dec 26, 2022) www.youtube.com/watch?v=mhkX1VArlT0.
[9] K. von Bloh. Bohm Trajectories for the Anisotropic Coulomb Potential with Constant Phase Shift: Part 2 [Video]. (Dec 26, 2022) www.youtube.com/watch?v=mmNFFvksa8Q.
Snapshots
Permanent Citation