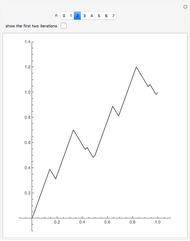
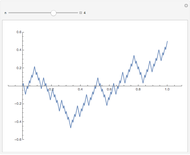
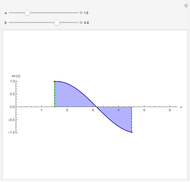
Bolzano's Theorem
Initializing live version
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
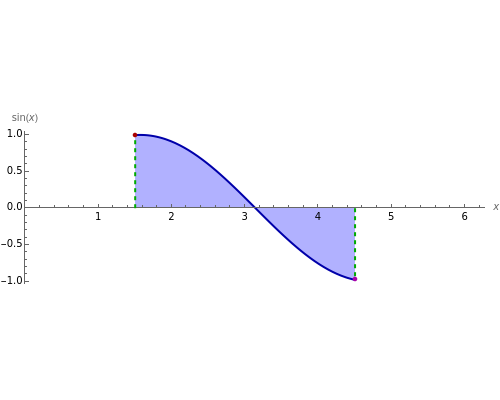
Bolzano's theorem states that if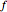 
is a continuous function in the closed interval 
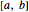with 
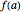and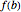 
of opposite sign, then there is a 
in the open interval 
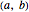such that 
.
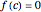Contributed by: Julio Cesar de la Yncera (May 2008)
Open content licensed under CC BY-NC-SA
Details
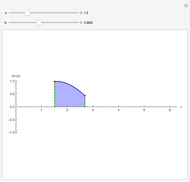
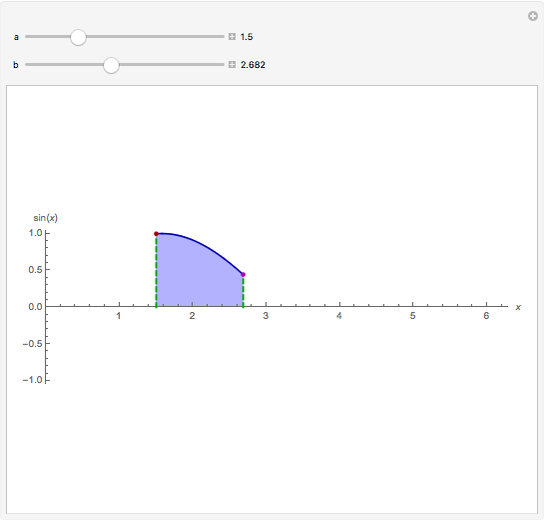
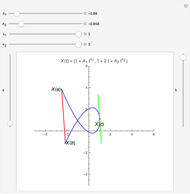
Snapshot 1: The function is positive in the interval and therefore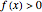 
for all 
in 
.
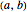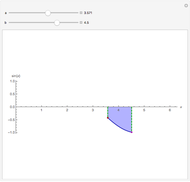
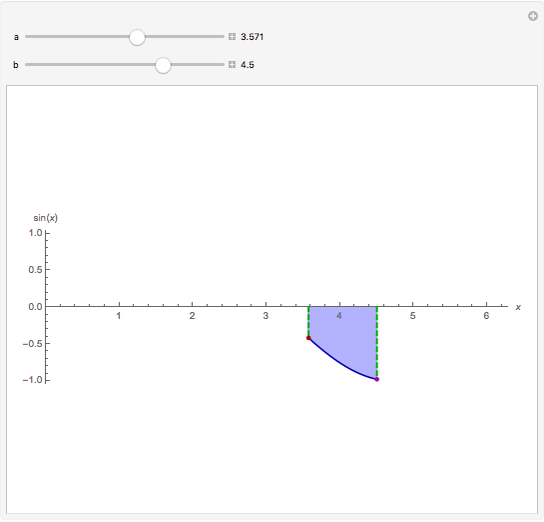
Snapshot 2: The function is negative in the interval so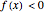 
for all 
in 
.
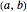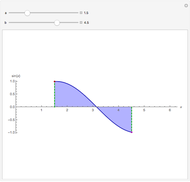
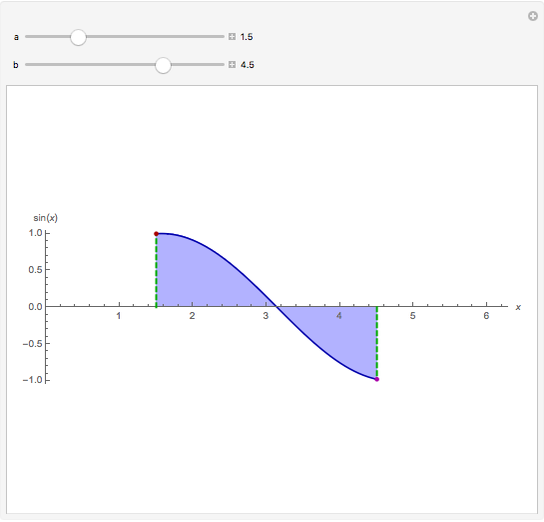
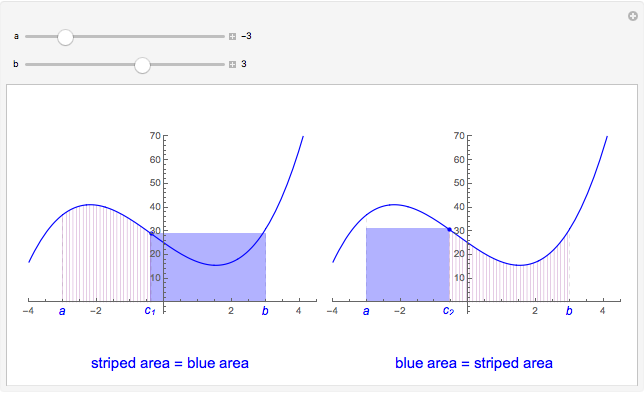
Snapshot 3: The function is positive for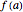 
and negative for 
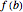, therefore there is a 
in 
such that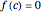 
.
Snapshots
Permanent Citation
Related Demonstrations
More by Author
Fermat's Theorem on Stationary Points
Julio Cesar de la Yncera
Cauchy Mean-Value Theorem
Soledad Mª Sáez Martínez and Félix Martínez de la Rosa
Two Integral Mean Value Theorems
Soledad María Sáez Martínez and Félix Martínez de la Rosa
Two Integral Mean Value Theorems of Flett Type
Soledad María Sáez Martínez and Félix Martínez de la Rosa
Marden's Theorem
Bruce Torrence
Squeeze Theorem
Bruce Atwood (Beloit College)
Lucas-Gauss Theorem
Bruce Torrence
2D and 3D Views of the Weierstrass Function
Daniel de Souza Carvalho
Bolzano's Function
Izidor Hafner
Bolzano's Continuous but Nowhere Differentiable Function
Izidor Hafner
