Bootstrap Percentile Confidence Intervals

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
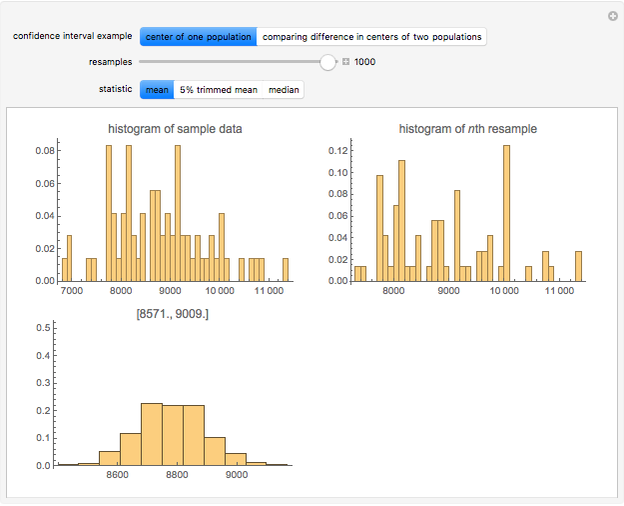
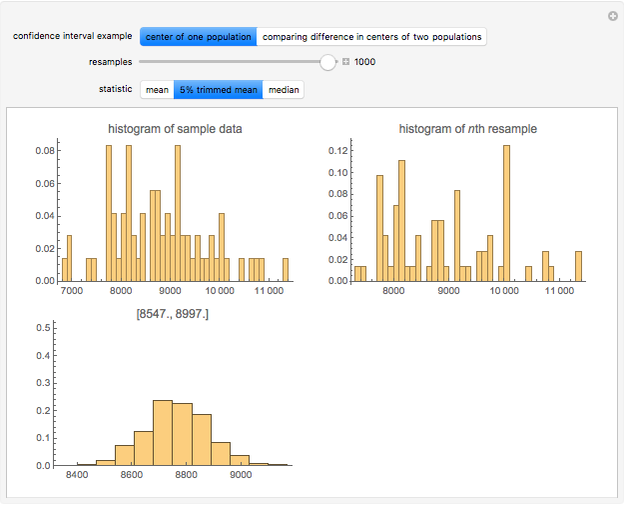
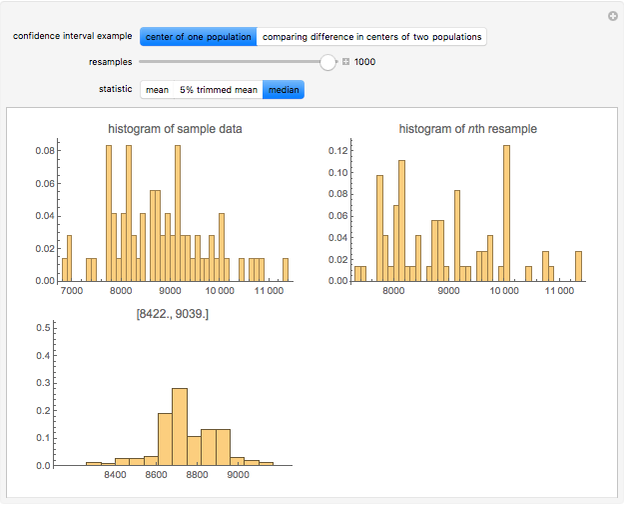
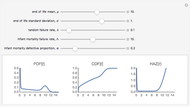
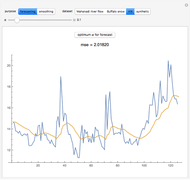
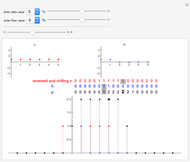
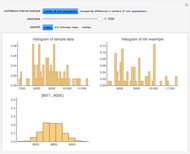
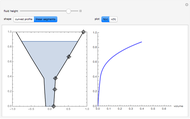
Bootstrapping is a technique for finding confidence intervals directly by resampling. The first histogram shows the original sample. The second histogram is the 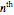 resample drawn from the original sample with replacement. The third histogram is the bootstrap (or resampling) distribution of the statistic calculated from the
resample drawn from the original sample with replacement. The third histogram is the bootstrap (or resampling) distribution of the statistic calculated from the 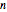 resamples. Above the third histogram is the bootstrap percentile confidence interval (the central 95% of the bootstrap distribution). In all the histograms the bin height is the fraction of values in that bin.
resamples. Above the third histogram is the bootstrap percentile confidence interval (the central 95% of the bootstrap distribution). In all the histograms the bin height is the fraction of values in that bin.
Contributed by: Sijia Liang and Bruce Atwood (August 2011)
(Beloit College)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The one-population data is from 72 monthly totals of accidental deaths in the United States. The two-populations data is from body weights in kg of 97 male and 47 female cats. For the two-populations example the third histogram compares the two groups by calculating for each pair of resamples the difference between the statistic applied to the resample of the male cats minus the statistic applied to the resample of the female cats. Both datasets are from the example data included with Mathematica.
Resampling techniques such as bootstrapping have been growing in popularity since they can sometimes be used for samples that are small or not normal. Bootstrap confidence intervals can be calculated even when the distribution of a statistic is unknown or complicated.
Students should ask themselves why the bootstrap distribution for the median of the two-populations example realizes only certain values. Do you think that the confidence interval for the difference in medians is reliable for this particular example?
Permanent Citation
"Bootstrap Percentile Confidence Intervals"
http://demonstrations.wolfram.com/BootstrapPercentileConfidenceIntervals/
Wolfram Demonstrations Project
Published: August 30 2011