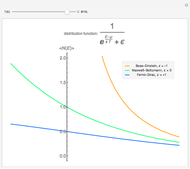
Bose-Einstein, Fermi-Dirac, and Maxwell-Boltzmann Statistics

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
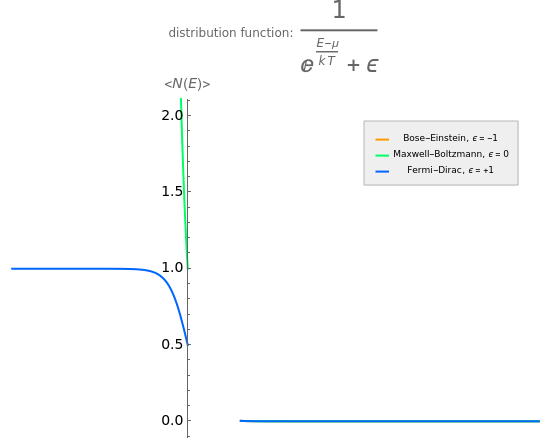
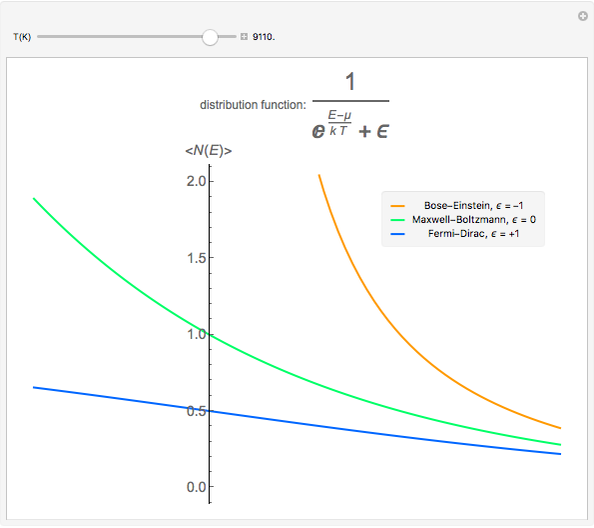
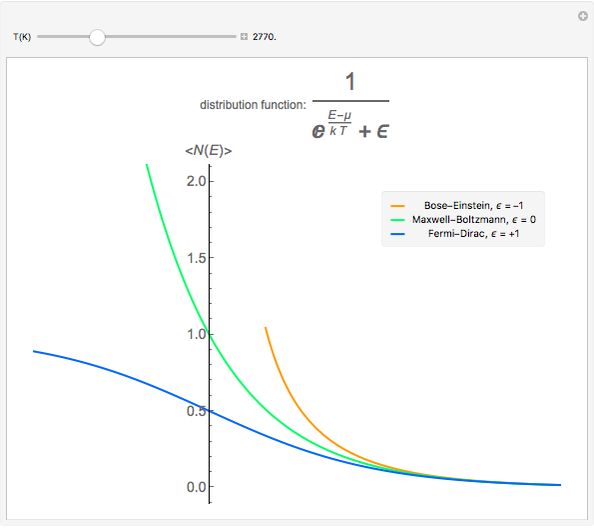
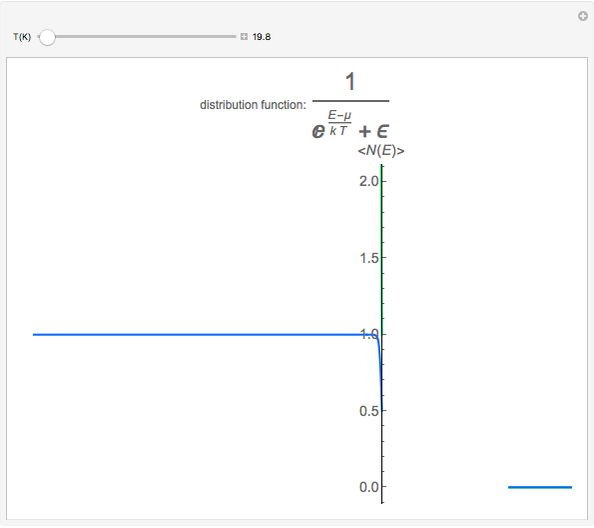
Maxwell–Boltzmann statistics apply where quantum-mechanical effects do not play a role and the particles of the gas can be considered "distinguishable". Both Fermi–Dirac and Bose–Einstein statistics become Maxwell–Boltzmann statistics at high temperatures and low chemical potentials where 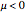 .
.
Contributed by: Christian Freier (University of Technology Berlin) (March 2011)
Open content licensed under CC BY-NC-SA
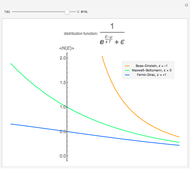
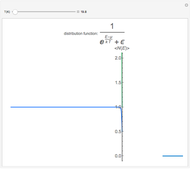
Snapshots
Details
detailSectionParagraphPermanent Citation
"Bose-Einstein, Fermi-Dirac, and Maxwell-Boltzmann Statistics"
http://demonstrations.wolfram.com/BoseEinsteinFermiDiracAndMaxwellBoltzmannStatistics/
Wolfram Demonstrations Project
Published: March 7 2011