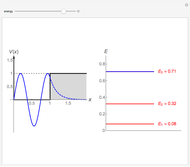
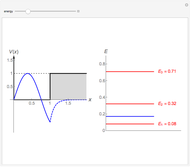
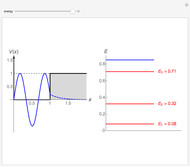
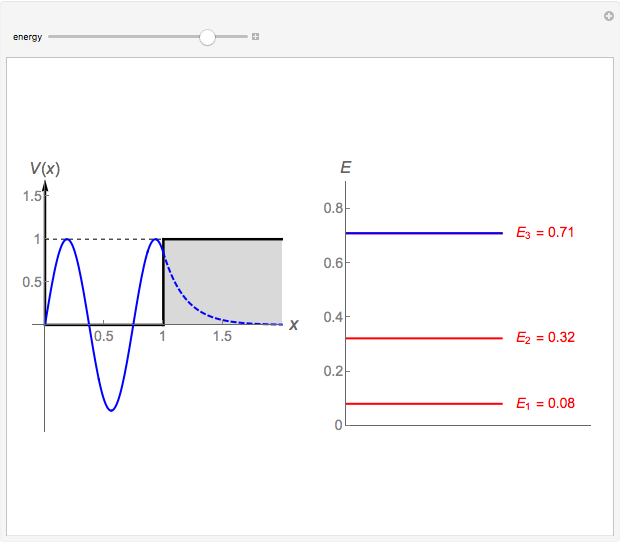
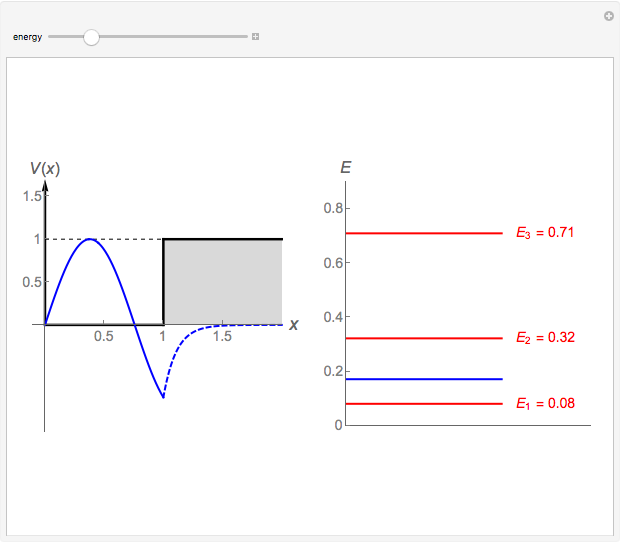
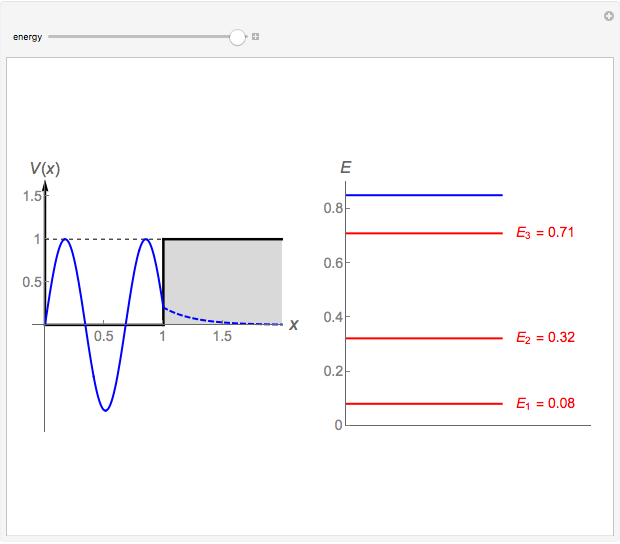
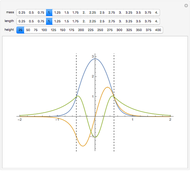
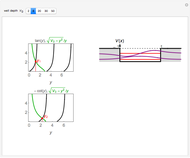
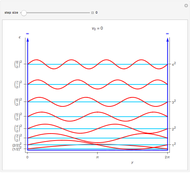
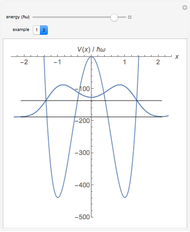
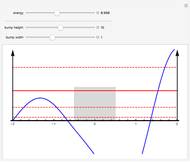
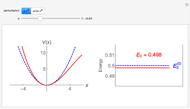
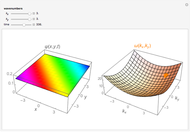
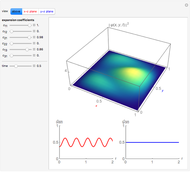
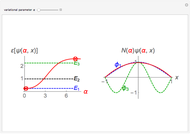
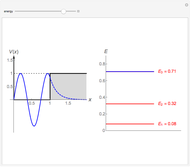
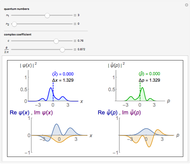
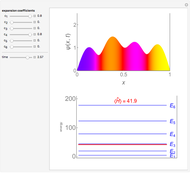
This Demonstration shows the solutions to the time-independent Schrödinger equation, treating energy as a continuous parameter. Once appropriate boundary conditions are applied, the energy levels become quantized and the corresponding eigenfunction and its first derivative are continuous across the boundary. The left and right panels show the wavefunction and corresponding energy, respectively. If the energy is equal to one of its eigenvalues, the wavefunction is smooth across the boundary; otherwise it develops a kink.