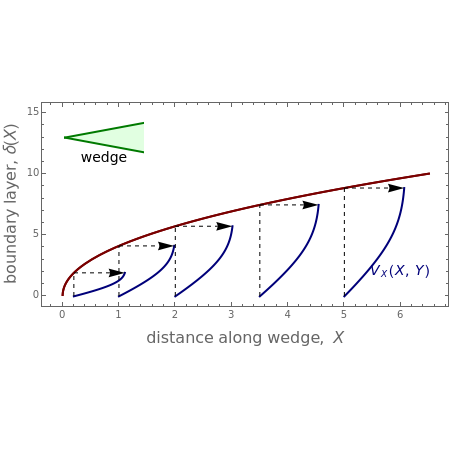
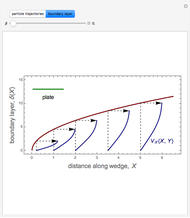
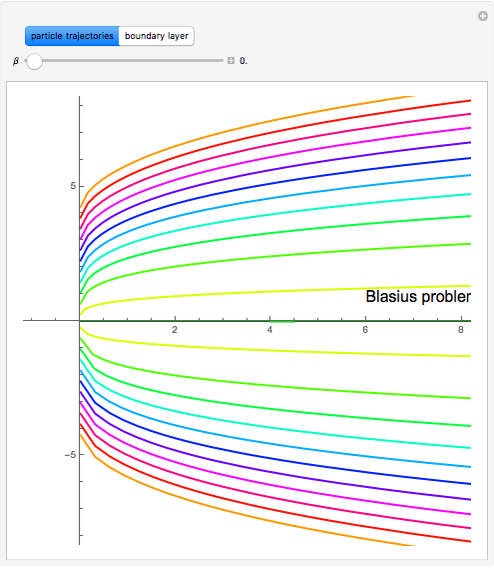
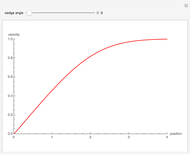
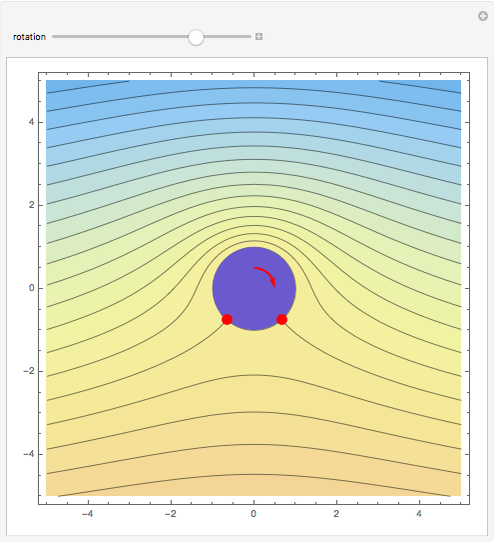
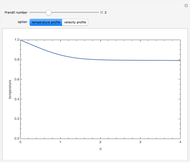
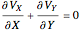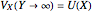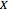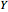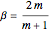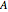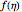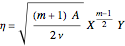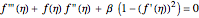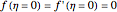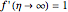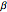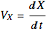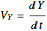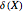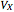Boundary-Layer Flow Past a Semi-Infinite Wedge: The Falkner-Skan Problem

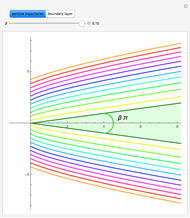
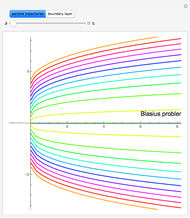
In 1904 Prandtl showed that the effects of viscosity at a high Reynolds number could be represented by approximating the Navier–Stokes equations with the celebrated boundary-layer equations, which for two-dimensional steady flow reduce to:

Here, and are the coordinates parallel and perpendicular to the body surface, respectively.

For a semi-infinite wedge with an angle of taper , one can prove that far from the wedge the potential flow is given by

, where or , and is a scale factor.

The above boundary-layer equations admit a self-similar solution such that the velocity profiles at different distances can be made congruent with suitable scale factors for and . This reduces the boundary-layer equations to one ordinary differential equation.

Let us introduce a function such that: where .

Then, we have from continuity equation: .

The boundary-layer equations can be written as follows:

with and

The above equation can be solved for a user-set value of parameter when and using the shooting technique. The limiting case is flow over a flat plate (Blasius problem). Using the following definitions of and , one can obtain the particle trajectories (streamlines) for different starting points. This Demonstration plots such trajectories and also shows the growth of the boundary-layer (red curve) in a separate plot for any value of the wedge angle. The evolution of the -velocity component and its congruent properties with the growth of the boundary layer is also shown.