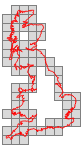
Box-Counting the Dimension of Coastlines

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
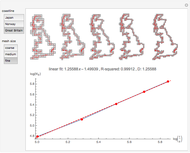
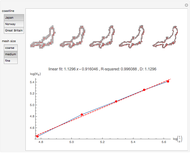
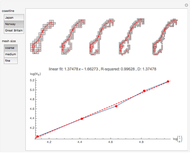
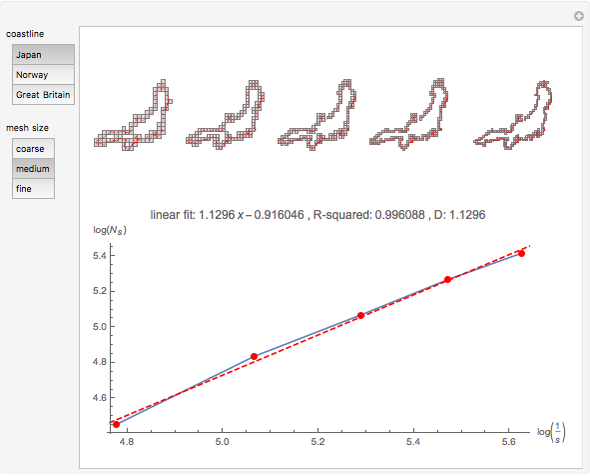
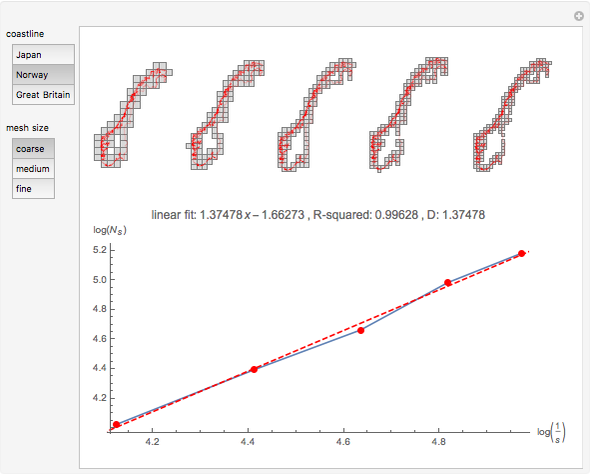
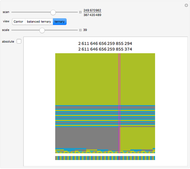
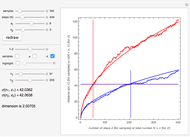
This Demonstration uses the box-counting method [1] to estimate the fractal dimension of three coastlines. The box-counting dimension of a coastline can be computed using a mesh of evenly spaced squares laid over a map of the coastline.
[more]
Contributed by: Erik Mahieu (January 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
References
[1] V. Kaurov. "Measuring Fractal Dimension of Natural Object from Digital Images." Mathematica Stack Exchange. (Oct 16, 2012) mathematica.stackexchange.com/questions/13125/measuring-fractal-dimension-of-natural-objects-from-digital-images.
[2] M. Mitchell et al. "Introduction to Complexity: 3.6 Box-Counting Dimension." Complexity Explorer. (2013) www.complexityexplorer.org/online-courses/3.
Permanent Citation