Breadth-First Search Robot Motion Planning

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
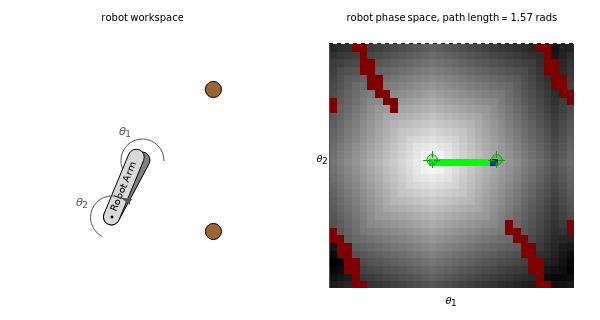
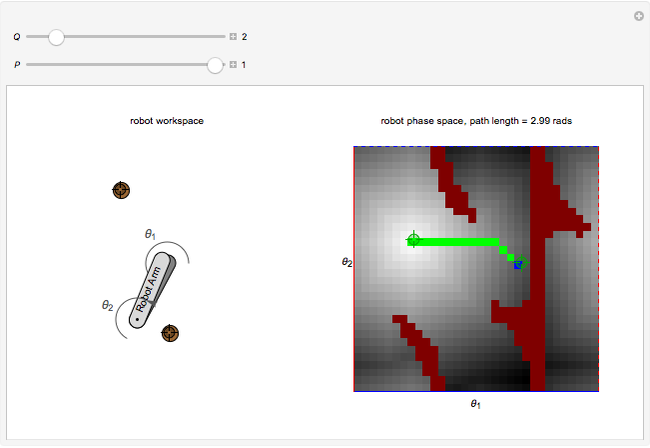
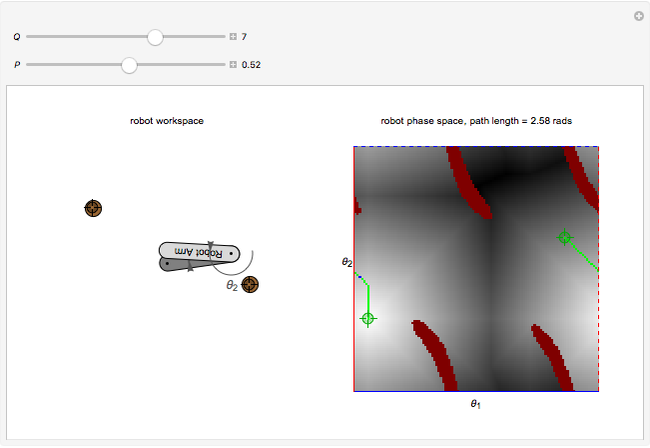
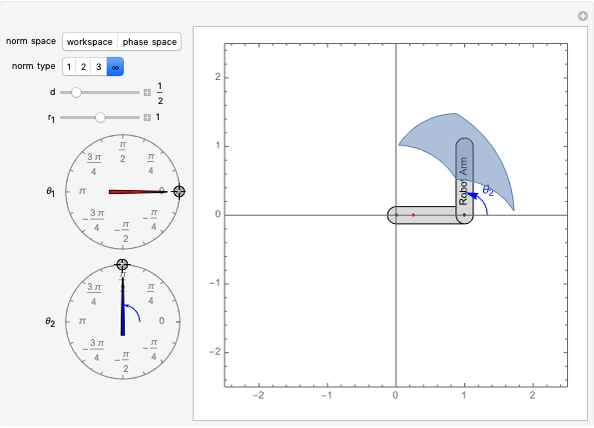
This Demonstration shows a resolution-complete planner that finds the shortest path between an initial and final configuration of a two-link, planar-arm robot by using a breadth-first search. The robot operates in the workspace on the left that contains two small circular obstacles. The corresponding robot phase space on the right shows the configurations 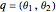 , for which an arm intersects an obstacle. You can relocate obstacles in the workspace and change the initial and final positions. You can improve the resolution of the search grid by increasing
, for which an arm intersects an obstacle. You can relocate obstacles in the workspace and change the initial and final positions. You can improve the resolution of the search grid by increasing  and move the robot along the shortest path by increasing
and move the robot along the shortest path by increasing 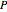 .
.
Contributed by: Aaron T. Becker, Benedict Isichei and Praveen Reddy Padala (December 2017)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The set of all possible configurations of a two-link, planar-arm robot can be represented in a two-dimensional phase space. Of particular interest are the configurations in which the robot collides with one of the obstacles. A resolution-complete planner returns a path between the initial and final configuration if it exists or returns that such a path is impossible. The path is discovered using breadth-first search in the phase space, which calculates the distance to every configuration reachable from the initial configuration. In this Demonstration, path distance is shown by a gradient that darkens with distance from the initial configuration. Even if configurations are close in the configuration space, obstacles may make moving between them require a longer distance.
This Demonstration computes the obstacle regions using 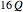 unit squares and determines if the centroid of each square is in a collision. Given
unit squares and determines if the centroid of each square is in a collision. Given 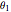 and
and 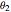 , one collision computation is trivial.
, one collision computation is trivial.
However, computing the phase-space obstacle region is more difficult because the size of the space representation grows exponentially with the number of degrees of freedom (independent joints) of the robot.
Consider how many  -dimensional unit squares are required to fill a space of size
-dimensional unit squares are required to fill a space of size  . For a one-dimensional space,
. For a one-dimensional space, 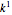 units are needed. For a two-dimensional space,
units are needed. For a two-dimensional space, 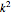 squares are needed. For an
squares are needed. For an  -dimensional space,
-dimensional space, 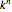 hypercubes would be required. The number of collision computations grows exponentially with the number of joints in the robot, making breadth-first search computationally infeasible for robots with many joints.
hypercubes would be required. The number of collision computations grows exponentially with the number of joints in the robot, making breadth-first search computationally infeasible for robots with many joints.
The phase space for a two-link, planar robot can be represented on a torus. When rotation joint 1 moves past 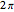 , it returns to angle 0. This is represented by dashed and solid lines of the same color. If the phase space were printed on a rubber sheet and cut out and the dashed and solid lines of each color were joined, the resulting shape would be a torus. In this Demonstration, moving the locator past the edge of the phase space wraps the angle around
, it returns to angle 0. This is represented by dashed and solid lines of the same color. If the phase space were printed on a rubber sheet and cut out and the dashed and solid lines of each color were joined, the resulting shape would be a torus. In this Demonstration, moving the locator past the edge of the phase space wraps the angle around 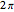 .
.
Reference
[1] M. Spong, S. Hutchinson and M. Vidyasagar, Robot Modeling and Control, Hoboken, NJ: John Wiley & Sons, 2006.
Permanent Citation