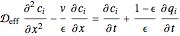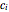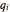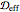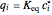An important unit operation in biotechnology and chemical engineering is fixed-bed adsorption.
Species to be separated, called separands, are either in the mobile phase or adsorbed by the stationary phase. The separands are subject to convection, mechanical dispersion, and molecular diffusion.
A mass balance, obtained by considering a disk of cross-sectional area equal to that of the column, gives:
,
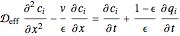where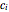
and
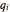are the concentrations of the separand in the mobile and stationary phases, respectively,
is the void fraction of the column,
is the mobile phase superficial velocity,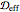
is the effective dispersivity of the separand in the column,
is the longitudinal position in the column, and finally
is time.
Since linear equilibrium is assumed: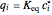
. Also consider that mass transfer resistances are negligible (i.e.,
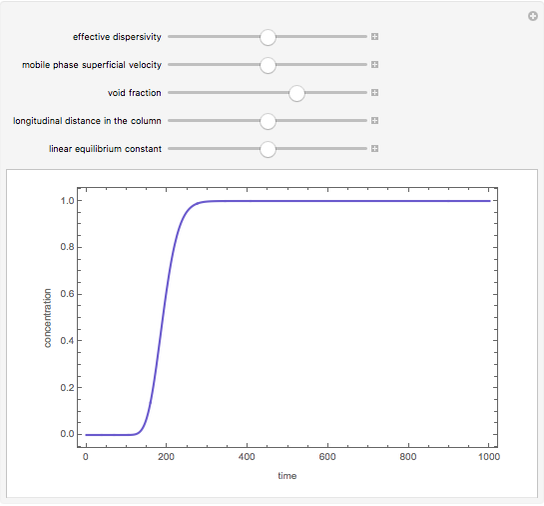
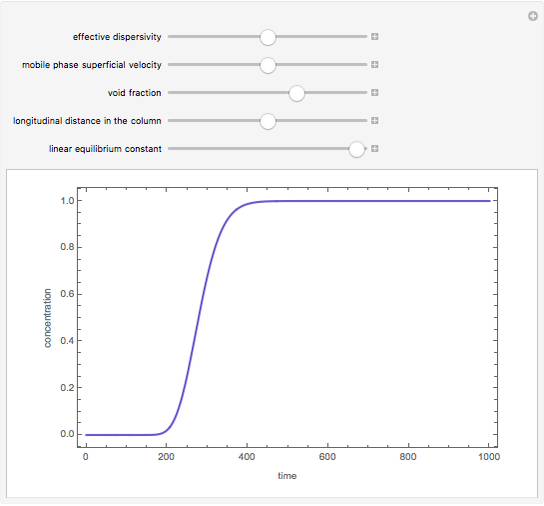
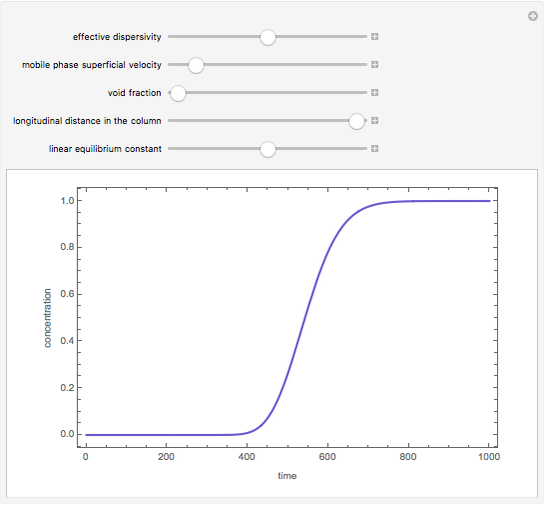
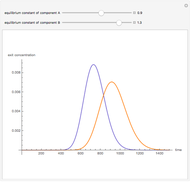
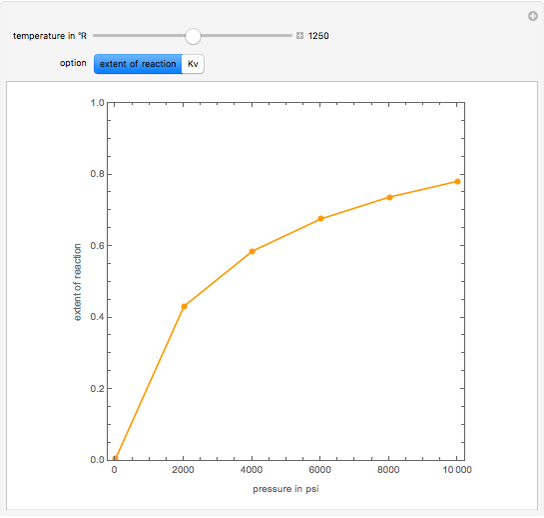
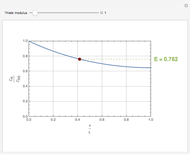
The breakthrough curve, the separand concentration versus time at the exit of the column, can be determined experimentally or computed numerically. In the present Demonstration, breakthrough curves are computed for a variety of values of the relevant parameters.
Browse all topics
