Buoyancy, Gravity, and Drag on a Sphere Immersed in a Liquid

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
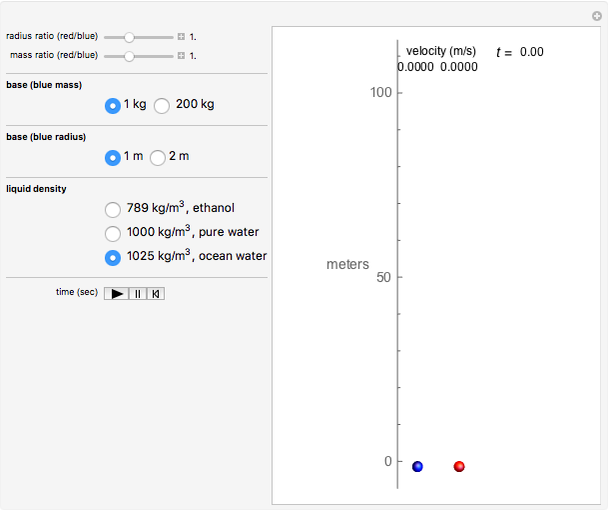
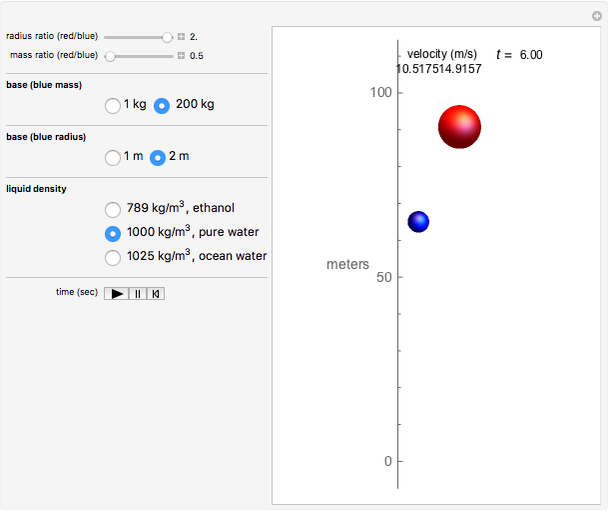
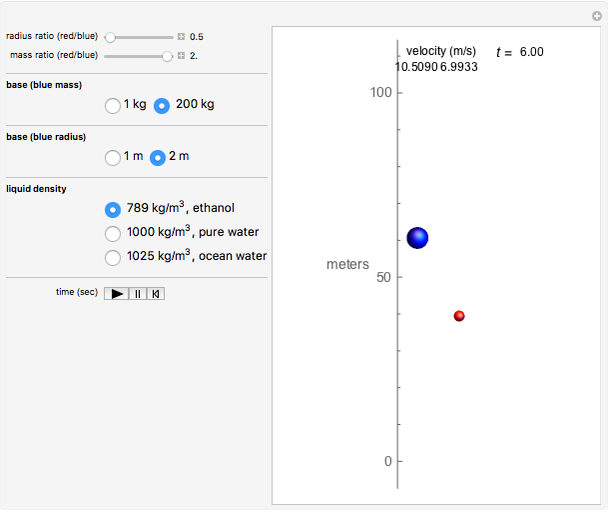
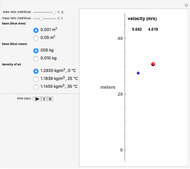
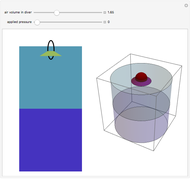
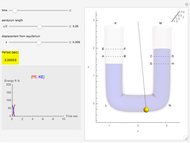
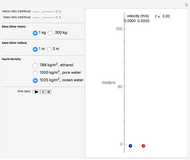
This Demonstration shows the velocity and position as functions of time for two spheres immersed in a liquid, rising under the influence of the forces of buoyancy, gravity, and drag. You can vary the base mass and radius of the blue sphere, and also the red sphere's mass and radius relative to the blue sphere. The spheres start out at the bottom, defined as 0 meters on the scale, and travel upward to a height of 100 meters, where they will have achieved terminal velocity.
Contributed by: Conrad Benulis (August 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
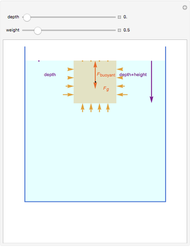
The motion is described by the force equation:
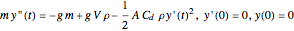 .
.
The forces are due to gravity, buoyancy, and drag, which appear in that order in the above differential equation. The Demonstration restricts the controls to make certain that the spheres are buoyant. The buoyant force acts upward, while gravity acts downward, as does the drag, which acts as a retarding force proportional to the square of the velocity. When the upward and downward forces reach equilibrium, a terminal velocity is attained.
Permanent Citation
"Buoyancy, Gravity, and Drag on a Sphere Immersed in a Liquid"
http://demonstrations.wolfram.com/BuoyancyGravityAndDragOnASphereImmersedInALiquid/
Wolfram Demonstrations Project
Published: August 14 2012