Buying Watermelons Intelligently

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
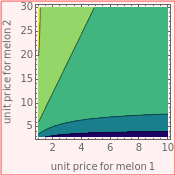
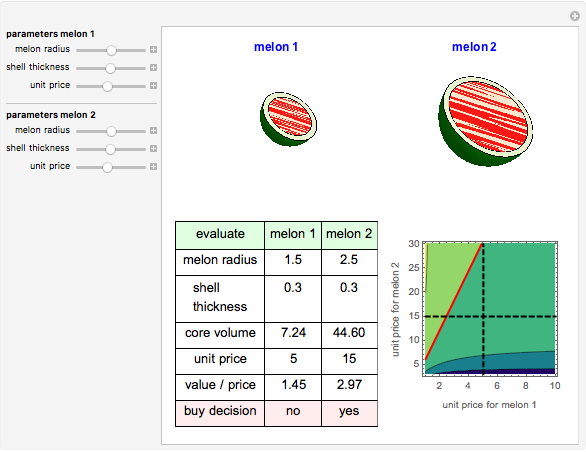
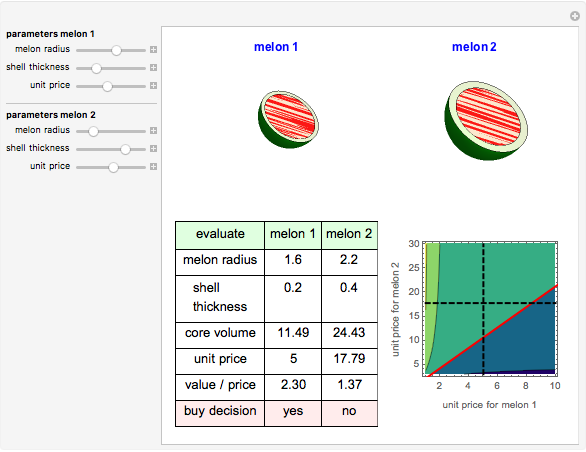
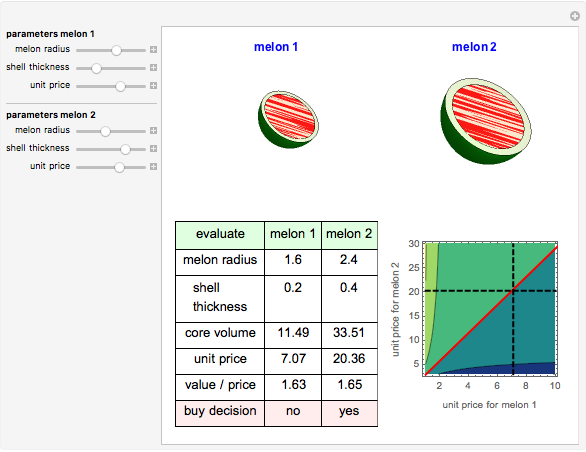
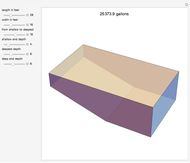
Millions of tons of watermelons are consumed each summer worldwide. People eat only the sweet red core of a watermelon. Stores set different prices depending on the size of the melons. How do you buy them intelligently? This Demonstration calculates core volume and shows the most economical solution for consumers.
Contributed by: Frederick Wu (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
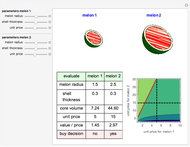
Snapshot 1: shows that buying big melon (2) is more economical than buying small melon (1).
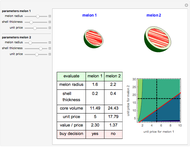
Snapshot 2: shows that buying small melon (1) is more economical than buying big melon (2).
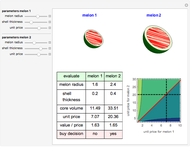
Snapshot 3: shows that buying small melon (1) is almost the same as buying big melon (2).
There is an interesting true story that comes from a Chinese mathematician, Wang Yuan. One summer afternoon, he and his wife went to buy watermelons. The watermelon salesman classified the melons into two groups, big and small, selling the big melons for 15 yuan each and the small melons for 5 yuan each. Mr. Wang and his wife looked at both groups of melons. Mr. Wang said, "Let's buy a big one." Mrs. Wang said, "That is three times the price of the smaller one. If we buy one big one, we could also buy three small ones." Wang thinks, "The big one is a better value. Look, we eat the core of the melon. The volume is proportional to the cube of the radius." Mrs. Wang nodded and said, "However, the big one has more shell." Mr. Wang said, "The small ones also have shells; let's calculate the volume of each shell." Mrs. Wang smiled and said, "Oh, I have a headache. I quit. Okay, we buy a big one." They bought two big watermelons and went home happily, leaving the salesman still thinking.
For more details, see Chapter 2 of F. Wu, Manipulate@Mathematica, Beijing, Tsinghua, 2010.
Permanent Citation
"Buying Watermelons Intelligently"
http://demonstrations.wolfram.com/BuyingWatermelonsIntelligently/
Wolfram Demonstrations Project
Published: March 7 2011