Capitalization Rate Probability

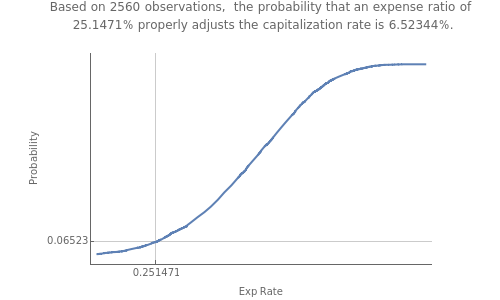
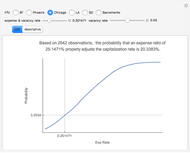
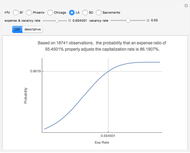
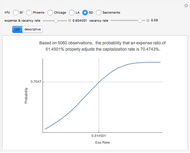
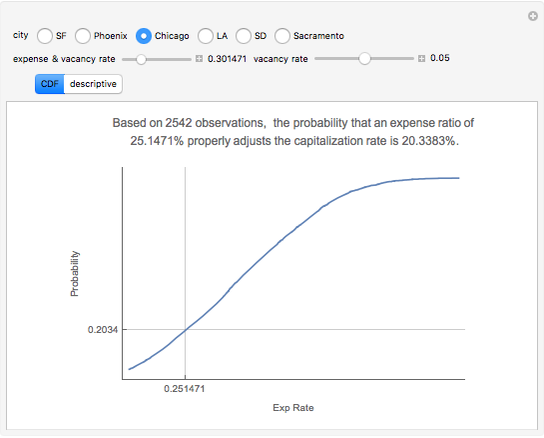
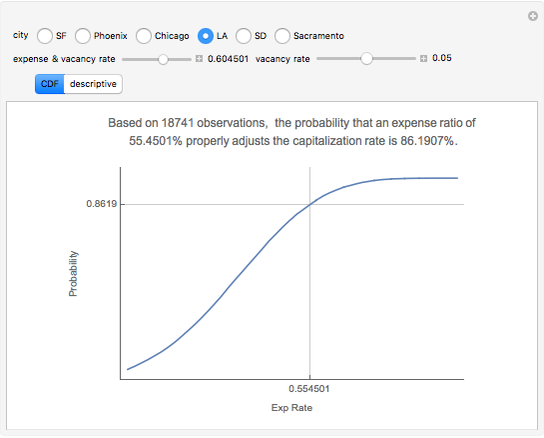
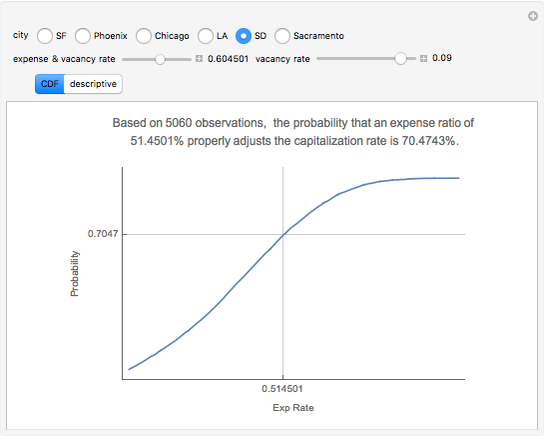
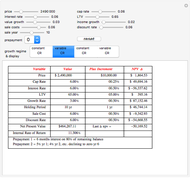
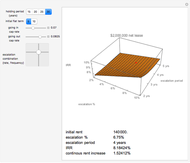
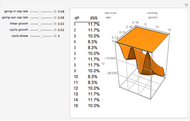
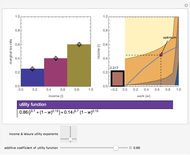
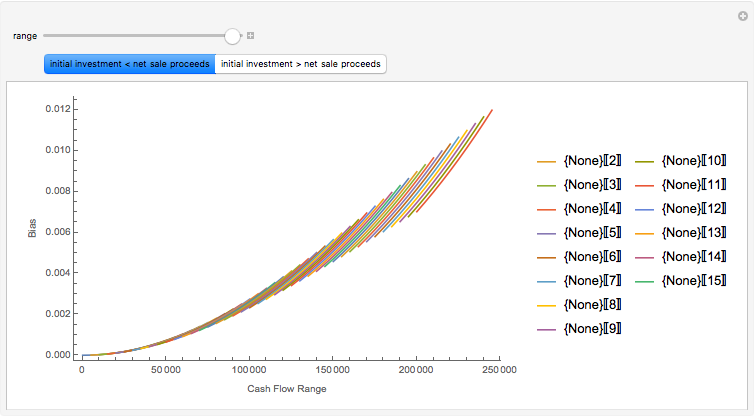
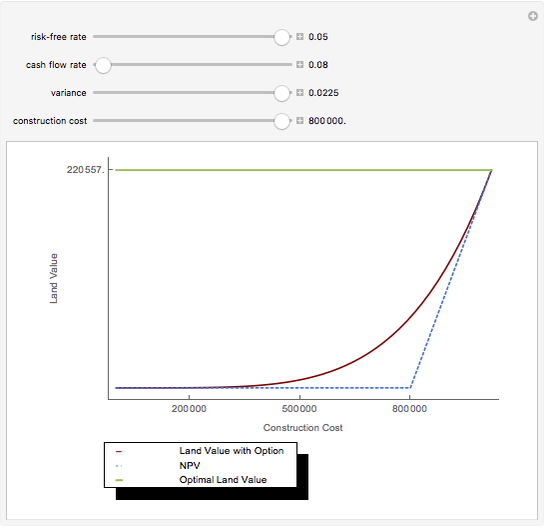
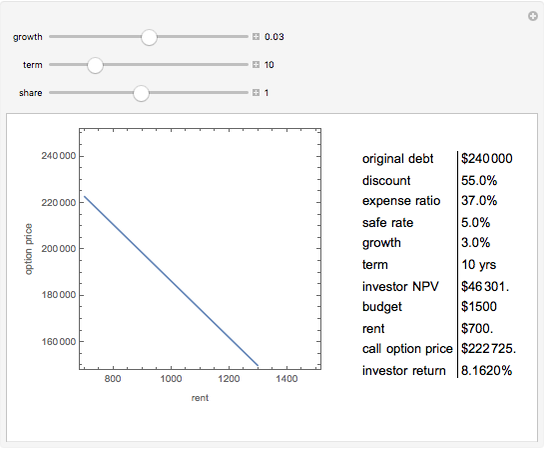
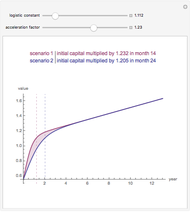
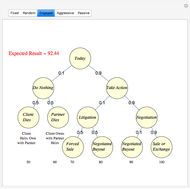
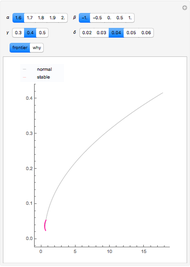
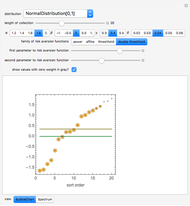
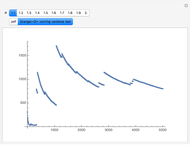
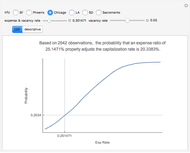
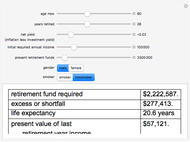
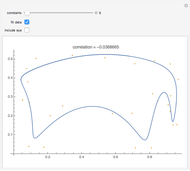
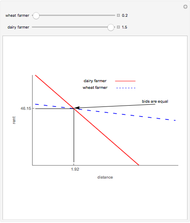
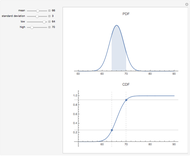
Capitalization rate (CR) is very sensitive to assumptions made about operating expenses when calculating net income. Statistical analysis of a variable, named "expense and vacancy rate" (EVR), can provide guidance. Happily, deriving EVR employs two of the most accurate characteristics in a real estate dataset: gross income and value. These two variables combine to make the gross rent multiplier (). EVR is the result of subtracting the product of GRM and the capitalization rate from one, thus .

As the vacancy rate is widely reported for most urbanized areas, it can be subtracted from EVR to arrive at the expense rate. This Demonstration provides actual GRM and CR data for six major U.S. cities, derives the EVR, and allows the user to specify a level of vacancy to be deducted. The empirical CDF places the expense rate in a probability context. As one would expect, low expense ratios used to balloon CR to an unrealistic level are improbable.

The "descriptive" tab displays the usual descriptive statistics.