Carnot Cycles with Irreversible Heat Transfer

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
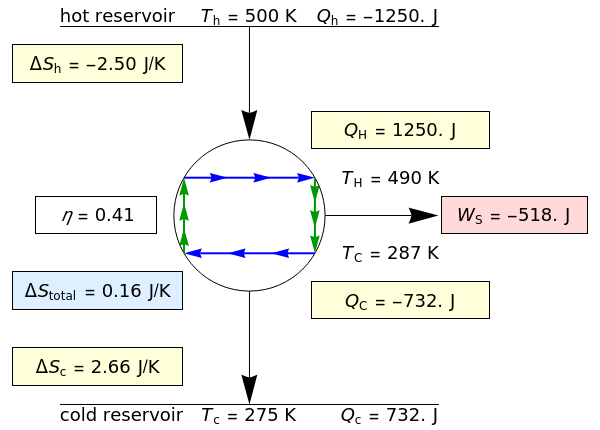
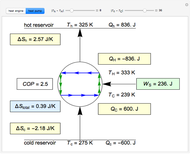
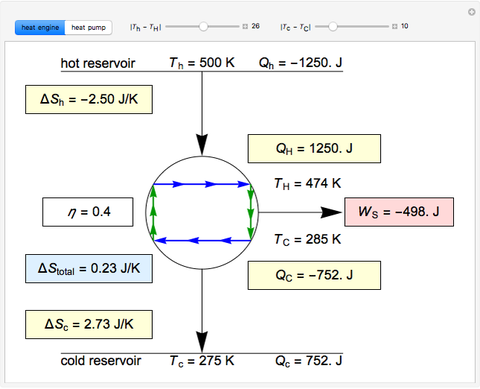
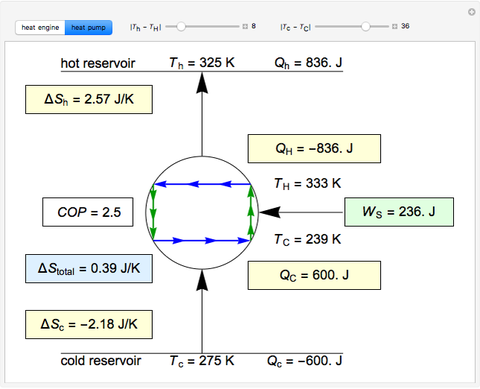
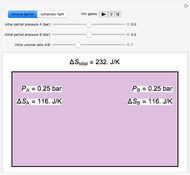
This Demonstration models a Carnot cycle as either a heat engine or a heat pump. Change the temperature differences between the reservoirs and the Carnot cycle with sliders. The entropy changes for the reservoirs (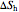 and
and 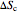 ) and the overall entropy change
) and the overall entropy change  are calculated. When the temperature differences between the reservoirs and the engine/pump are zero, the total entropy change is zero and the process is reversible. The entropy change of the engine/pump, which is at steady state, is zero. All energies and entropy changes are per unit time, since these are continuous processes, but the time scale is arbitrary. The cycle efficiency
are calculated. When the temperature differences between the reservoirs and the engine/pump are zero, the total entropy change is zero and the process is reversible. The entropy change of the engine/pump, which is at steady state, is zero. All energies and entropy changes are per unit time, since these are continuous processes, but the time scale is arbitrary. The cycle efficiency  is calculated for the heat engine, and the coefficient of performance
is calculated for the heat engine, and the coefficient of performance  is calculated for the heat pump. As the temperature differences between the reservoirs and the engine/pump increase, the efficiency/coefficient of performance decreases. For the heat engine,
is calculated for the heat pump. As the temperature differences between the reservoirs and the engine/pump increase, the efficiency/coefficient of performance decreases. For the heat engine, 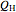 is held constant at 1250 J, and for the heat pump,
is held constant at 1250 J, and for the heat pump, 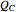 is held constant at 600 J.
is held constant at 600 J.
Contributed by: Rachael L. Baumann (July 2014)
Additional contributions by: Megan Maguire, John L. Falconer, and Nick Bongiardina
(University of Colorado Boulder, Department of Chemical and Biological Engineering)
Open content licensed under CC BY-NC-SA
Snapshots
Details
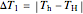 ,
,
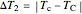 ,
,
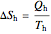 ,
,
 ,
,
 ,
,
where 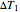 and
and 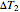 are user-defined differences in reservoir and Carnot cycle temperatures (K). The subscripts
are user-defined differences in reservoir and Carnot cycle temperatures (K). The subscripts 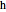 and
and  refer to the hot or cold reservoirs, and the subscripts
refer to the hot or cold reservoirs, and the subscripts 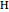 and
and  refer to the hot or cold temperatures of the Carnot cycle.
refer to the hot or cold temperatures of the Carnot cycle. 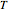 is temperature (K),
is temperature (K), 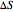 is the change in entropy (J/K), and
is the change in entropy (J/K), and 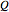 is heat gained or lost (J).
is heat gained or lost (J).
For a Carnot heat engine, heat is transferred from a hot reservoir to a cold reservoir and the engine does work (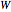 ). For a real process,
). For a real process,  and
and 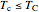 . The efficiency
. The efficiency  of a Carnot engine, in terms of the engine temperatures, is:
of a Carnot engine, in terms of the engine temperatures, is:
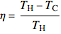 ,
,
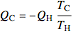 ,
,
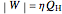 .
.
For a Carnot heat pump, heat is transferred from the cold reservoir to the hot reservoir and work is added. For a real process, 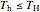 and
and 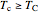 to have a reasonable rate of heat transfer. The coefficient of performance
to have a reasonable rate of heat transfer. The coefficient of performance  is
is
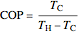 ,
,
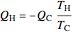 ,
,
 .
.
The screencast video at [2] explains how to use this Demonstration.
References
[1] J. R. Elliott and C. T. Lira, Introductory Chemical Engineering Thermodynamics, New York: Pearson Education, 2012 pp. 157–158.
[2] Carnot Cycle with Irreversible Heat Transfer. www.colorado.edu/learncheme/thermodynamics/CarnotCycles.html.
Permanent Citation