Catching a Point within a Teragon

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
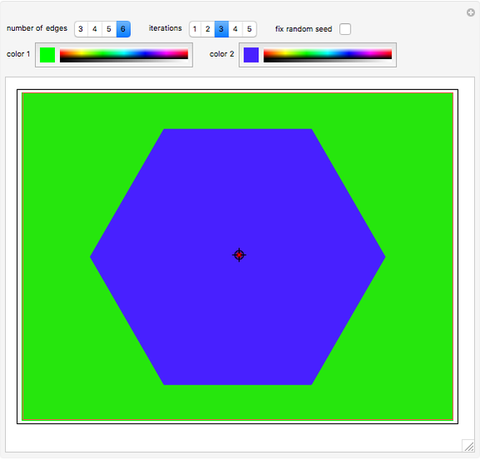
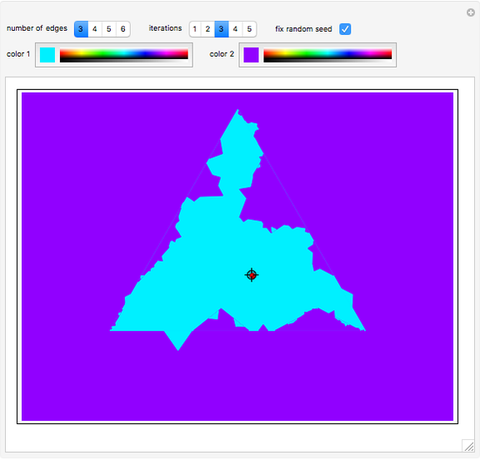
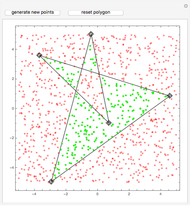
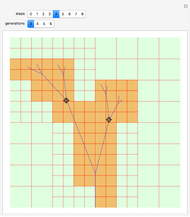
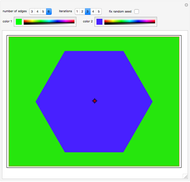
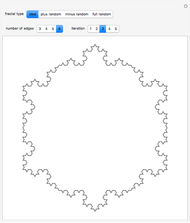
This Demonstration presents a solution to the problem of determining if a chosen point of a two-dimensional plane, selected using the locator, is within the region bounded by a regular convex polygon whose edges are replaced with randomized Koch curves. This region is a self-similar fractal curve called a teragon [1]. The internal and external areas exchange colors as the point crosses the boundary.
Contributed by: Vasil Saroka (September 2017)
Open content licensed under CC BY-NC-SA
Snapshots
Details
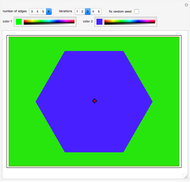
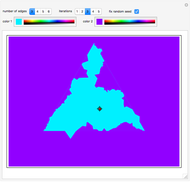
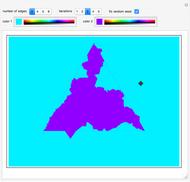
The region containing the given point is "color 1", while the remaining area is "color 2". Both colors can be customized.
Snapshot 1: the point is inside the teragon
Snapshot 2: the point is outside the teragon
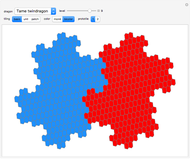
The given point represents the position of the atomic site in a two-dimensional crystal lattice. The teragon represents the boundary of a nanostructure referred to as a quantum dot. Thus, the teragon can be used as a mask that, when overlaid with the two-dimensional lattice, isolates a set of atomic sites forming a quantum dot with rough edges.
This approach has been used to model and study the edge roughness in phosphorene quantum dots [2]. It can also be readily applied to silicene quantum dots [3] or generalized to study edge disorder in other nanostructures, such as zigzag-shaped graphene nanoribbons [4–6].
References
[1] B. B. Mandelbrot, The Fractal Geometry of Nature, New York: W. H. Freeman, 1983.
[2] V. A. Saroka, I. Lukyanchuk, M. E. Portnoi and H. Abdelsalam, "Electro-optical Properties of Phosphorene Quantum Dots," Physical Review B, 96(8), 2017 085436. doi:10.1103/PhysRevB.96.085436.
[3] H. Abdelsalam, M. H. Talaat, I. Lukyanchuk, M. E. Portnoi and V. A. Saroka, "Electro-absorption of Silicene and Bilayer Graphene Quantum Dots," Journal of Applied Physics, 120(1), 2016 014304. doi:10.1063/1.4955222.
[4] V. A. Saroka and K. G. Batrakov, "Zigzag-Shaped Superlattices on the Basis of Graphene Nanoribbons: Structure and Electronic Properties," Russian Physics Journal, 59(5), 2016 pp. 633–639. doi:10.1007/s11182-016-0816-6.
[5] V. A. Saroka, K. G. Batrakov, V. A. Demin and L. A. Chernozatonskii, "Band Gaps in Jagged and Straight Graphene Nanoribbons Tunable by an External Electric Field," Journal of Physics: Condensed Matter, 27(14), 2015 145305. doi:10.1088/0953-8984/27/14/145305.
[6] V. A. Saroka, K. G. Batrakov and L. A. Chernozatonskii, "Edge-Modified Zigzag-Shaped Graphene Nanoribbons: Structure and Electronic Properties," Physics of the Solid State, 56(10), 2014 pp. 2135–2145. doi:10.1134/S106378341410028X.
Permanent Citation
"Catching a Point within a Teragon"
http://demonstrations.wolfram.com/CatchingAPointWithinATeragon/
Wolfram Demonstrations Project
Published: September 21 2017