Cauchy-Schwarz Inequality for Integrals

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
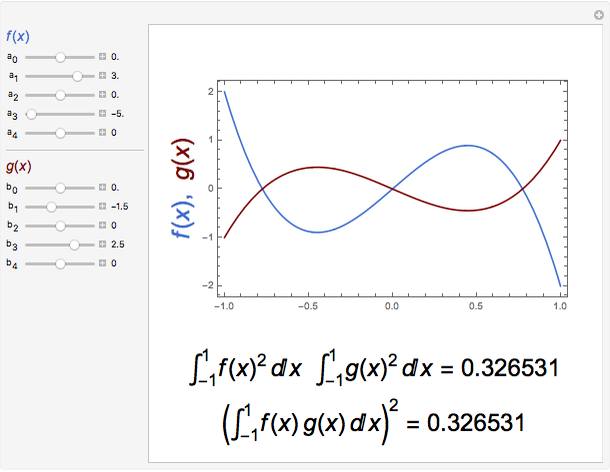
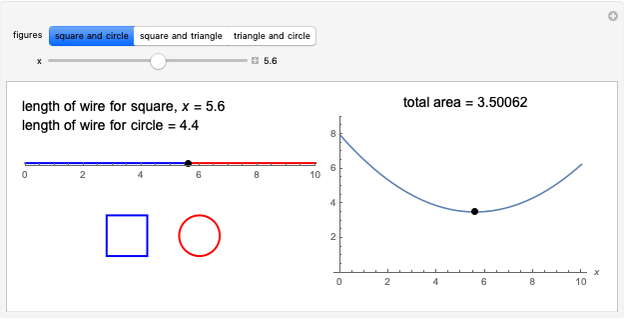
The Cauchy–Schwarz inequality for integrals states that 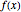 for two real integrable functions in an interval
for two real integrable functions in an interval 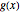 . This is an analog of the vector relationship
. This is an analog of the vector relationship  , which is, in fact, highly suggestive of the inequality expressed in Hilbert space vector notation:
, which is, in fact, highly suggestive of the inequality expressed in Hilbert space vector notation:  . For complex functions, the Cauchy–Schwarz inequality can be generalized to
. For complex functions, the Cauchy–Schwarz inequality can be generalized to 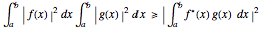 . The limiting case of equality is obtained when
. The limiting case of equality is obtained when 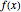 and
and 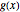 are linearly dependent, for instance when
are linearly dependent, for instance when  ).
).
Contributed by: S. M. Blinder (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
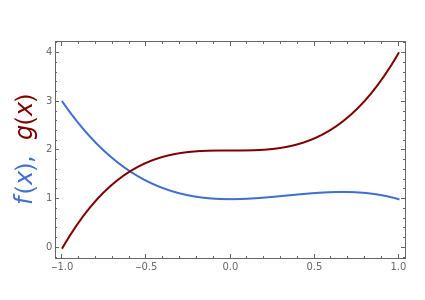
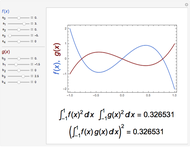
Snapshot 1: inequality of an order of magnitude
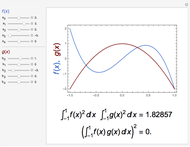
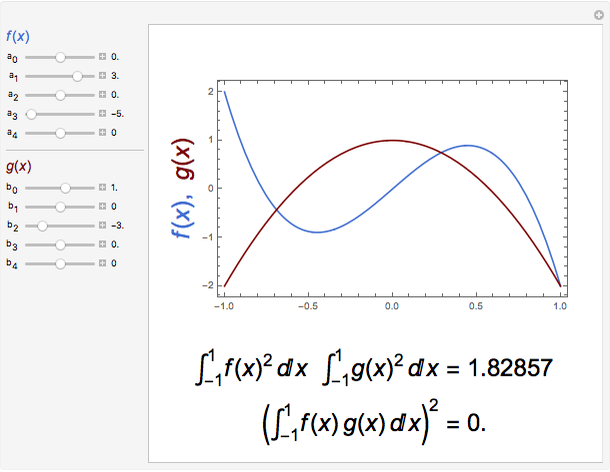
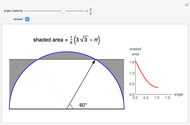
Snapshot 2: limiting case of equality since 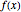 and
and 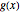 are proportional
are proportional
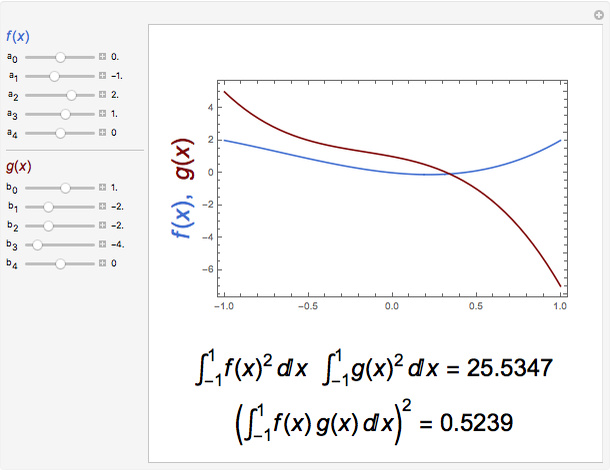
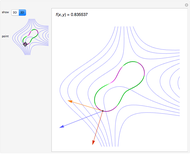
Snapshot 3: case of two orthogonal functions
Permanent Citation