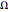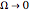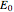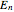Causal Interpretation of Transitions in a Two-Level System

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
The orthodox interpretation of transitions between quantum states in terms of discontinuous jumps is treated as an adjunct to the Schrödinger equation itself. In the causal interpretation, the particle position and momentum are well-defined and the transition can be described as a continuous evolution of the quantum particle according to the time-dependent Schrödinger equation. There are no "quantum jumps". To study transitions in a two-level system, time-dependent perturbation theory must be used. These solutions are not exact solutions of the Schrödinger equation, but they are extremely accurate. For the particular case of a two-level system perturbed by a periodic external field (but without quantization of the transition-inducing field and ignoring radiation effects), an accurate solution can be derived.
[more]
Contributed by: Klaus von Bloh (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
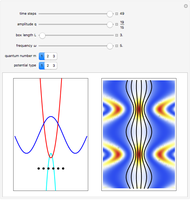
A two-level system is represented by a superposition of states in Dirac's bra-ket notation:
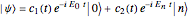 .
.
This leads to
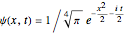
for the ground-state wavefunction. The 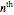 excited state, with energy
excited state, with energy 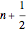 in dimensionless units, is correspondingly
in dimensionless units, is correspondingly
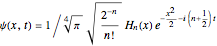 .
.
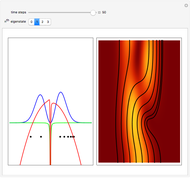
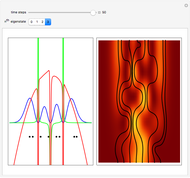
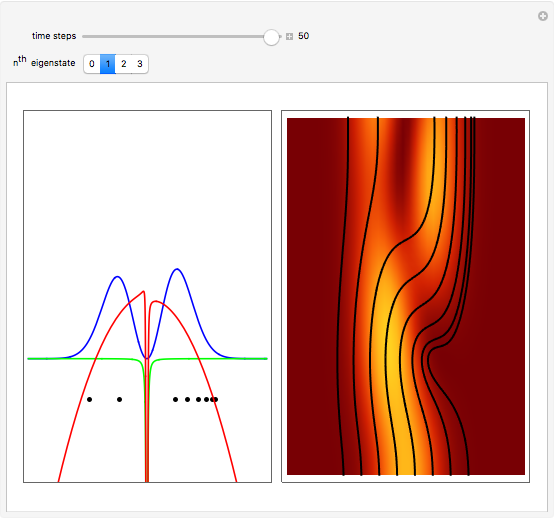
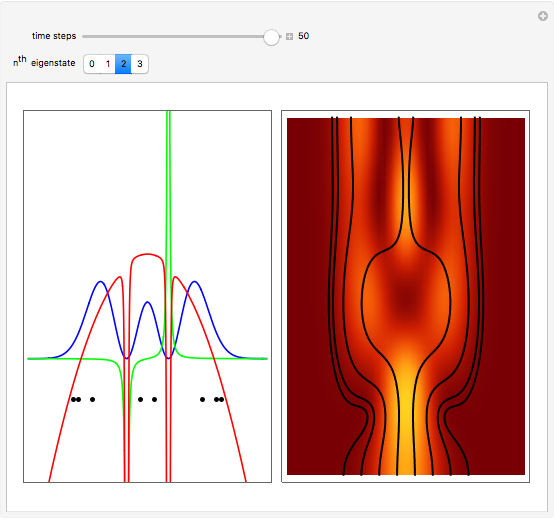
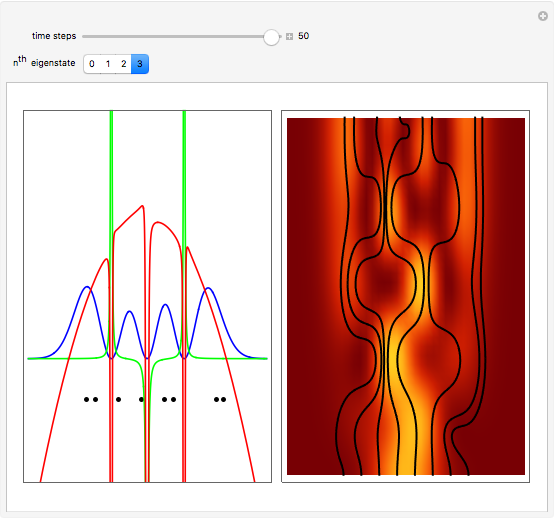
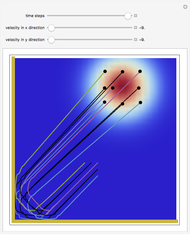
Inside the wave, the spatial starting points for the particles are linearly distributed around the peak. The velocity and quantum potential are appropriately scaled to fit.
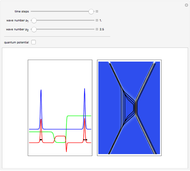
The graphic on the right shows the squared wavefunction and the trajectories. The one on the left shows the particle positions, the squared wavefunction (blue), the velocity (green), and the quantum potential (red).
Reference: C. Dewdney and M. M. Lam, "What Happens During a Quantum Transition?," Information Dynamics (H. Atmanspacher and H. Scheingraber, eds.), New York: Plenum Press, 1991.
Permanent Citation