Celestial Sphere Basics

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
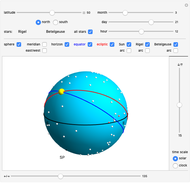
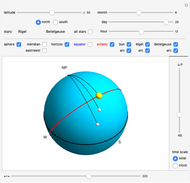
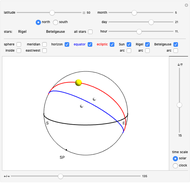
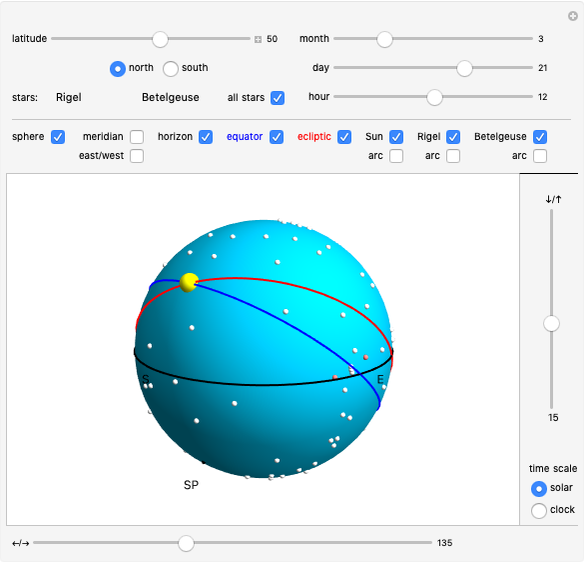
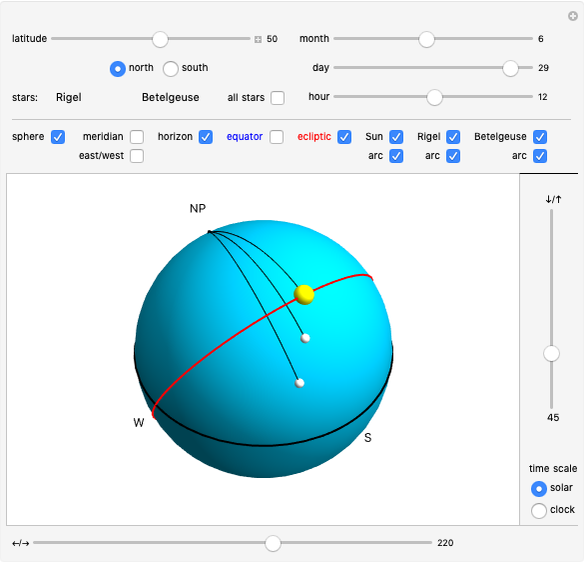
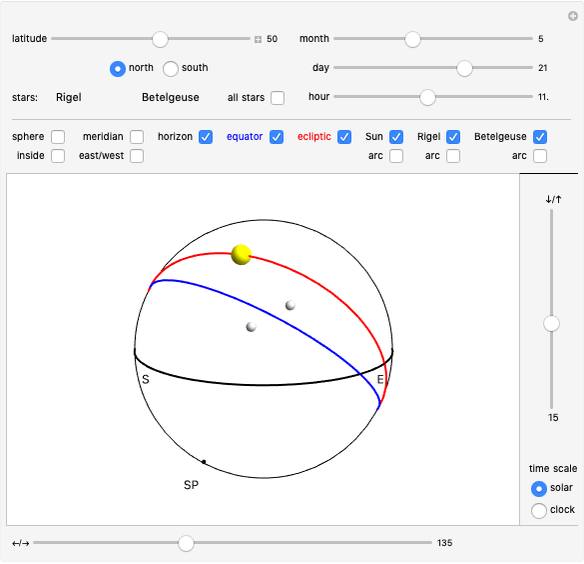
The celestial sphere is a model of the objects in the sky as viewed from an observer on Earth. The concept of the celestial sphere is often used in navigation and positional astronomy. The purpose of this Demonstration is to visualize the basic principles behind changes in the appearance of the celestial sphere, as it varies with the observer's latitude, time of year, and time of day.
[more]
Contributed by: Hans Milton (February 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The obliquity of the ecliptic is set to 23.4366°.
Tooltips show the coordinates of the Sun and two other selected stars. To see horizontal coordinates, mouseover the Sun or the star. Equatorial coordinates are shown when mousing over the arc from pole to the Sun or a star. Coordinate values are given in decimal notation. When an angle is given in the unit of hours it can be converted to degrees by multiplying by 15, that is, 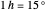 .
.
Horizontal coordinates shown in tooltips measure azimuth from North to East.
Hour angles shown in the tooltips are measured from the local meridian toward West. In the Northern Hemisphere, the zero hour angle is at local meridian South. In the Southern Hemisphere, the zero hour angle is at local meridian North.
In the collection of stars, one star is included that has no real counterpart. Named FP of Aries, its location is First Point of Aries. Its hour angle gives local sidereal time.
Local sidereal time is also shown in a tooltip when you mouse over the meridian arc.
Local sidereal time, hour angle and right ascension are related. Any two of the values determines the third: 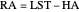 .
.
Two different time scales can be selected by radio buttons: solar and clock time. They correspond to Apparent Solar Time and Mean Solar Time, respectively. See [2]. In solar time, 24 hours is the interval between the Sun's successive appearances at the meridian. In clock time, 24 hours is the interval in which the celestial sphere rotates 361°. Solar and clock time coincide at equinoxes and solstices. To see the difference, select a day that is close to being halfway between an equinox and solstice.
Since this Demonstration uses a simplified model of the Earth's orbit, coordinate values differ from those given by an ephemeris table, but the difference is generally small for the purpose of locating a star in the sky.
For examples on the use of the celestial sphere in connection with spherical trigonometry, see [1].
References
[1] G. V. Brummelen, The Mathematics of the Heavens and the Earth: The Early History of Trigonometry, Princeton, NJ: Princeton University Press, 2009.
[2] Apparent and Mean Solar Time, https://en.wikipedia.org/wiki/Solar_time
Permanent Citation