Cellular Automata with Globally Determined Neighborhoods

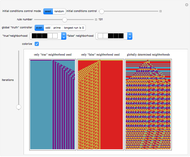
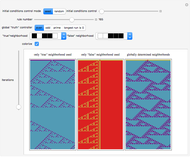
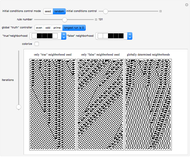
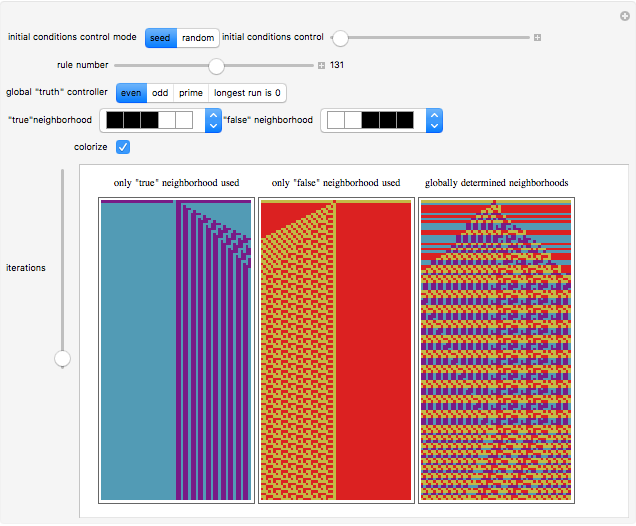
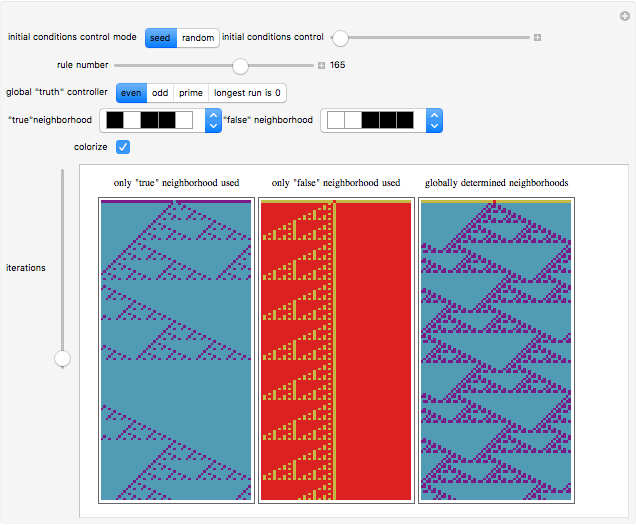
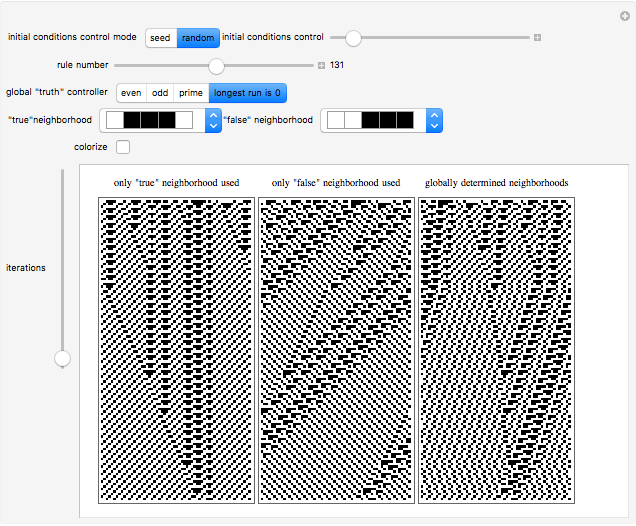
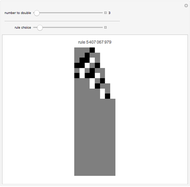
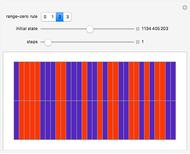
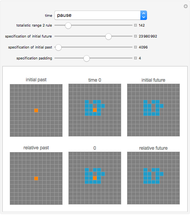
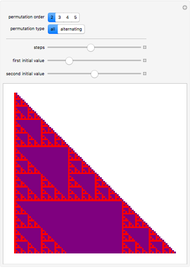
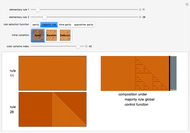
A cellular automaton with global control is one in which the evolution of the system depends not only on the states of each cell and its neighbors but also on some global feature of the system. This Demonstration examines cellular automata in which the global state of the system affects the neighborhoods that each cell examines in determining how to update itself. You choose the initial conditions for the system. In "seed" mode you select an initial state that is all zero except for some small seed. In "random" mode you select a random initial state. You then select one of 256 rules to apply. These are the conventional Wolfram elementary cellular automata. You select a "global truth controller" function. If the value of this function when applied to a row is True, then the neighborhood used to evolve each site on the next iteration is the one you select as the "true neighborhood". If the value of this function when applied to a row is False, then the neighborhood used to evolve each site on the next iteration is the one you select as the "false neighborhood". You also select the number of iterations examined. By checking "colorize" you can color-code the output depending on which neighborhood is being employed.