Central Limit Theorem for the Continuous Uniform Distribution
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
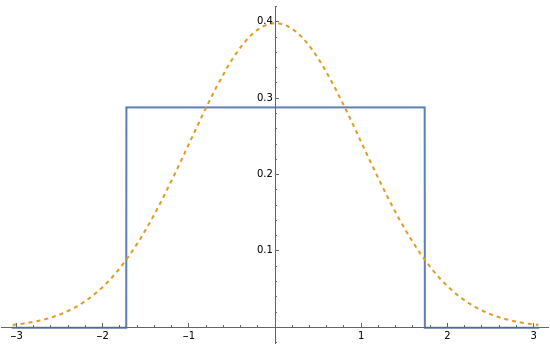
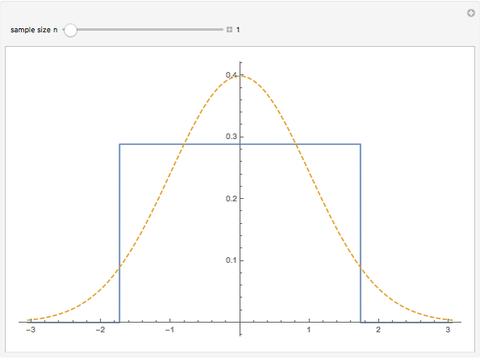
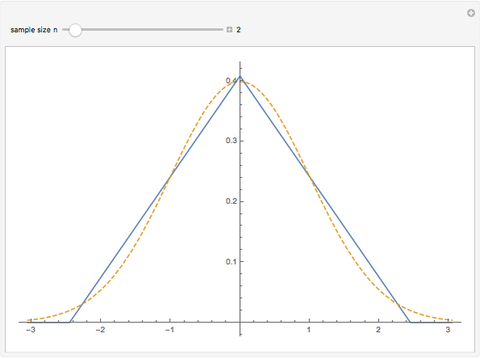
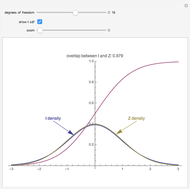
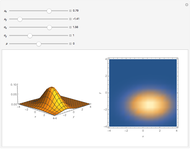
This Demonstration illustrates the central limit theorem for the continuous uniform distribution on an interval. If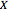 
has the uniform distribution on the interval 
and 
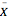is the mean of an independent random sample of size 
from this distribution, then the central limit theorem says that the corresponding standardized distribution 
approaches the standard normal distribution as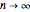 
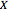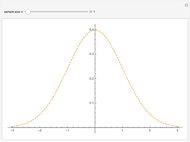
. Using operations on the characteristic function of we can compute the PDF of 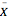more easily than we could directly. The blue curve is the PDF of and the dashed curve is the PDF of a standard normal distribution.
Contributed by: David K. Watson (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
If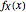 
is the PDF of a random variable 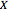, then 
, 
, (the convolution of 
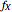and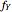 
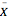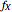). This means that finding the PDF of involves computing the -fold convolution of with itself, a computationally intensive operation to do directly even for small and simple PDF functions. This can be made easier in some cases by using the convolution property of Fourier transforms, 
, and the observation that the characteristic function of 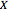is the same as the Fourier transform 
, which means that 
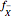can be computed by rescaling the inverse Fourier Transform of 
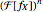. For the uniform distribution, this lets us compute the distribution for 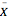much more quickly than we could directly, though it is still a little slow for larger .
Permanent Citation
The Central Limit Theorem
Chris Boucher
Central Limit Theorem Applied to Samples of Different Sizes and Ranges
Mark D. Normand and Micha Peleg
The Gamma Distribution
Chris Boucher
The Hypergeometric Distribution
Chris Boucher
The Chi-Squared Distribution
Chris Boucher
The Negative Binomial Distribution
Chris Boucher
Discrete Marginal Distributions
Chris Boucher
Illustrating the Use of Discrete Distributions
Nasser M. Abbasi
Student's t-Distribution
Chris Boucher
The Bivariate Normal Distribution
Chris Boucher
