Chain Puzzle on Triangular Grid

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
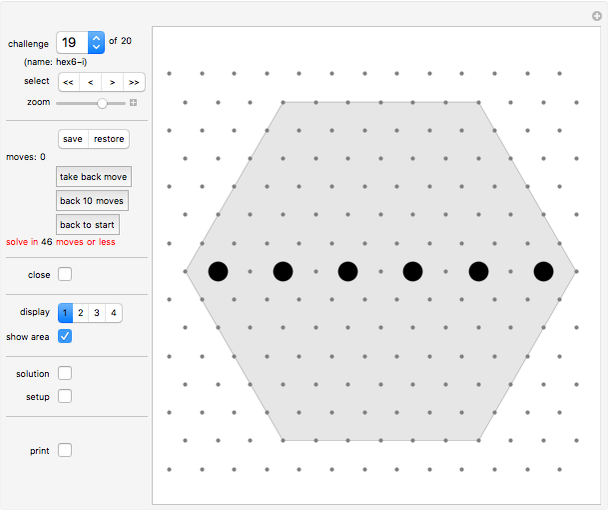
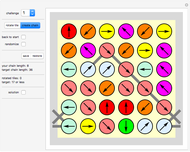
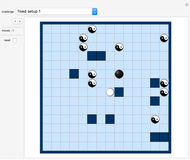
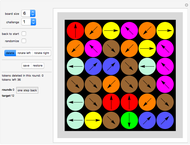
Object: Fill the board with a chain of connected rods. Each rod has to be one unit shorter or longer than the previous one. Various board layouts are given as challenges. Black dots mark no-go positions. You can also create your own board setups or vary an existing one.
Contributed by: Karl Scherer (January 2016)
Open content licensed under CC BY-NC-SA
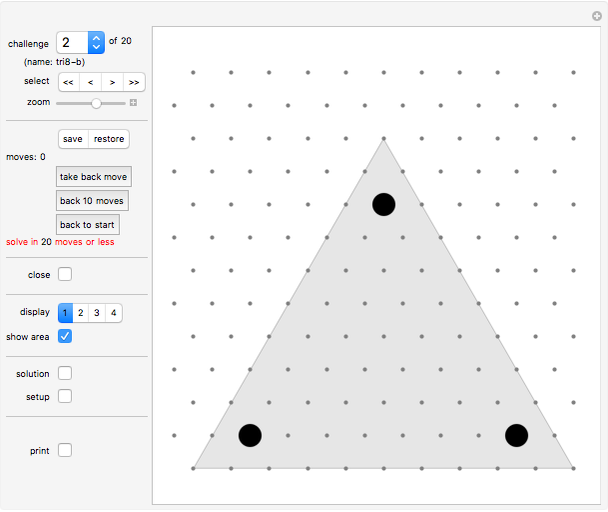
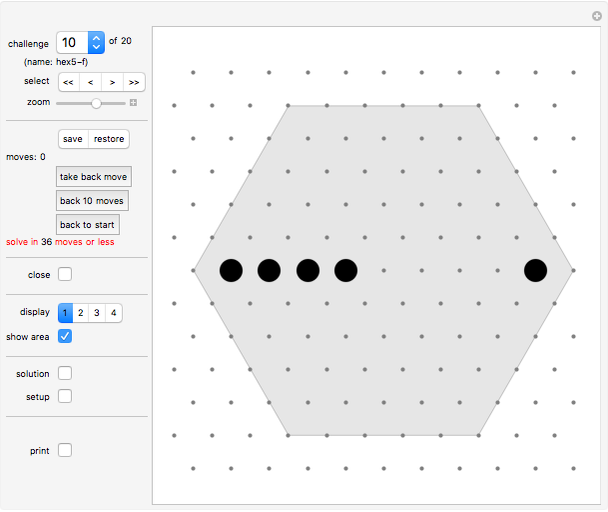
Snapshots
Details
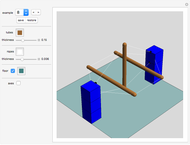
This game is played on a 60° grid.
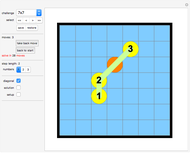
Click the board at any of the gray positions (dark dots, inside the black rim). A yellow circle marks the spot. Now click the board on another gray position in one of the six directions to display a new spot and a link connecting the spots. Keep clicking to create a chain of brown rods.
There is a special condition, however. The connection between the last link and the new link must be one unit longer or one unit shorter than the previous connection. For example, a rod of length 3 must be followed by a rod of length 2 or 4.
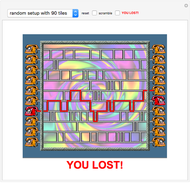
You win if you cover all points in the gray area with a continuous chain. You lose if you run out of moves. Some challenges have positions ("walls") marked by a black spot that you cannot go to or walk over. You can edit the set of walls at any time (see "setup" control below).
Note: the system does not check whether you click only inside the gray area. Also, there is no win message when you have filled the gray area.
Expert level
Once you have covered the board, try to do so with the least number of moves. All solutions have been found by hand by the author. Can you find shorter solutions?
Controls
The "challenge" pop-up menu and the "select" setter bar let you select a board.
The "zoom" slider sometimes is very handy in order to enlarge the board.
"save" stores the current board position; "restore" recalls it.
"moves" displays the number of moves you have played.
The "take back move" button lets you go back one move at a time.
"back 10 moves" lets you go back 10 moves at a time.
The "back to start" button takes you all the way back to the starting position.
"close" connects the last clicked position with the first clicked position, thereby creating a closed circuit. When "close" is active, no further editing is allowed. Note that this closing step also must follow the rule that its length is different from the lengths of the neighboring steps. Click "close" again to go back to editing mode.
Challenge: which of the given board setups can be solved with a closed circuit? Challenges 4 and 5 are examples with a closed-circuit solution.
"display 1" displays the sequence numbers of the links on the playing board.
"display 2" displays the board without numbers.
"display 3" displays the board as a "snake" of constant width.
"display 4" uses very thin rods.
"solution" all challenges come with a solution.
"setup" toggle: if activated, you can change the positions on the board that are walls (black dots). Click an empty board position to create a wall; click a wall to delete it.
History
A similar game, "Squared Chain Puzzle," was published by the same author as the Zillions game "Squared Chain" (and also as a Mathematica Demonstration) in 2015.
Permanent Citation
"Chain Puzzle on Triangular Grid"
http://demonstrations.wolfram.com/ChainPuzzleOnTriangularGrid/
Wolfram Demonstrations Project
Published: January 6 2016