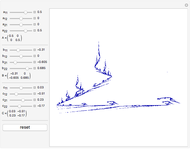
Chaos Game Fractals

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
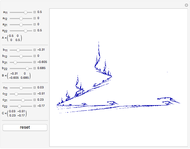
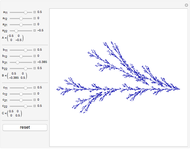
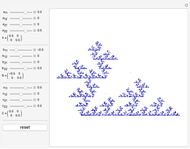
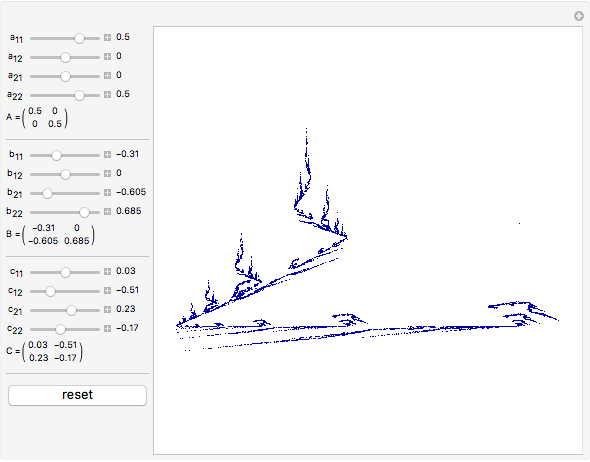
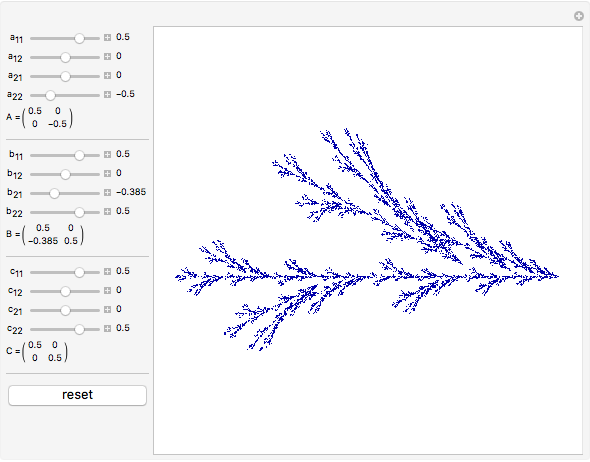
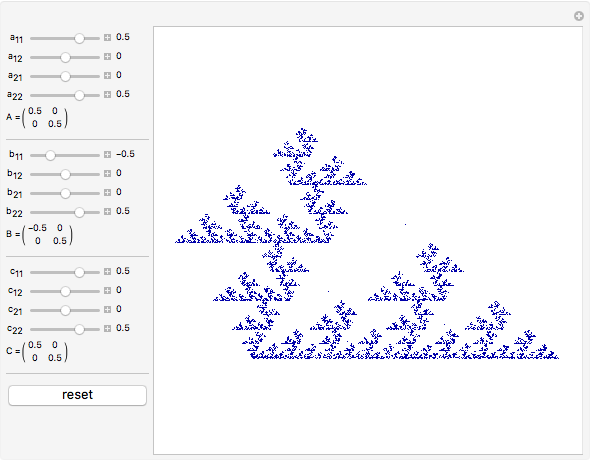
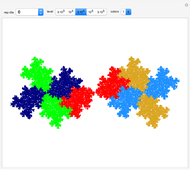
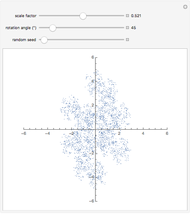
The chaos game is one method for generating fractals. First, mark the three vertices of an equilateral triangle and pick an initial point. Then randomly choose one of the vertices and move the point halfway to that vertex, marking where it lands. Repeat this, and eventually the points map out Sierpinski's triangle, regardless of what initial point is picked. We can generalize this process by picking a random affine transformation from a set and applying it to the vector that represents the initial point. We mark where the point lands, and repeat the process. This Demonstration lets you change the entries in three matrices, 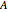 ,
, 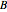 , and
, and 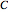 , that correspond to three linear transformations. After multiplying the vector by them, we add the vectors
, that correspond to three linear transformations. After multiplying the vector by them, we add the vectors 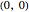 ,
, 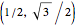 , and
, and  , respectively. There are 10,000 points plotted. The "reset" button moves the settings back to those that generate Sierpinski's triangle.
, respectively. There are 10,000 points plotted. The "reset" button moves the settings back to those that generate Sierpinski's triangle.
Contributed by: Sarah Peluse (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
R. L. Devaney, A First Course in Chaotic Dynamical Systems: Theory and Experiment, Boulder, CO: Westview Press, 1992.
Permanent Citation
"Chaos Game Fractals"
http://demonstrations.wolfram.com/ChaosGameFractals/
Wolfram Demonstrations Project
Published: March 7 2011