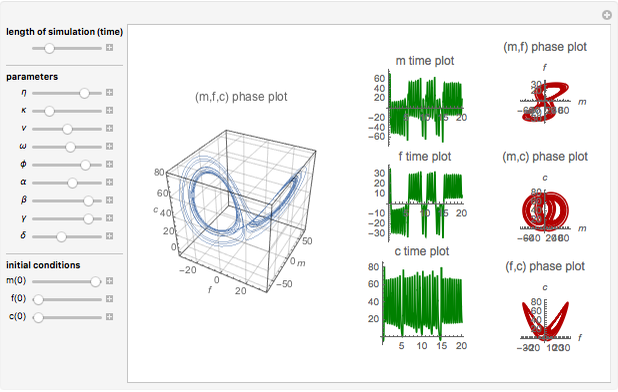
Chaotic Attractor in Tumor Growth

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
Model equations: 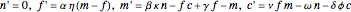 , where
, where  ,
, 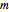 ,
, 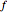 and
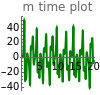
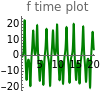
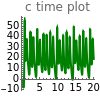
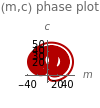
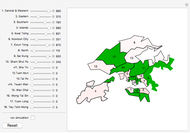
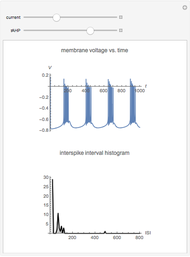
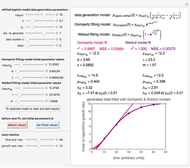
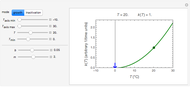
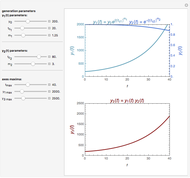
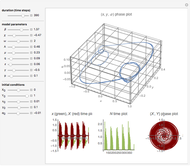
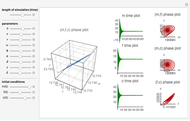
and  are functions of time that represent tumor cell density, MDE (mucinous ductal ectasia) concentration, MM (malignant melanoma) concentration and oxygen concentration, respectively. These temporal equations were derived from a reaction-diffusion model from the tumor growth. The model mathematically describes both the processes of carcinogenesis and metastasis, as well as the sensitive dependence of cancer evolution on initial conditions and parameters. On the basis of this chaotic cancer attractor, a generic concept of carcinogenesis and metastasis is formulated.
are functions of time that represent tumor cell density, MDE (mucinous ductal ectasia) concentration, MM (malignant melanoma) concentration and oxygen concentration, respectively. These temporal equations were derived from a reaction-diffusion model from the tumor growth. The model mathematically describes both the processes of carcinogenesis and metastasis, as well as the sensitive dependence of cancer evolution on initial conditions and parameters. On the basis of this chaotic cancer attractor, a generic concept of carcinogenesis and metastasis is formulated.
Contributed by: Tijana Ivancevic (March 2011)
Open content licensed under CC BY-NC-SA
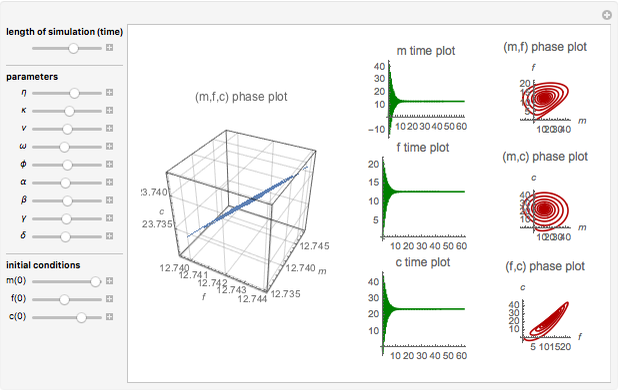
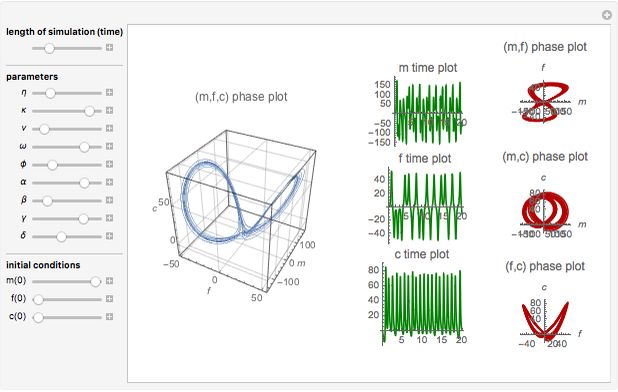
Snapshots
Details
Reference: T. T. Ivancevic, M. J. Bottema, and L. C. Jain, "A Theoretical Model of Chaotic Attractor in Tumor Growth and Metastasis," arXiv:0807.4272 in Cornell University Library's arXiv.org.
Permanent Citation