Chaotic Data: Delay Time and Embedding Dimension

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
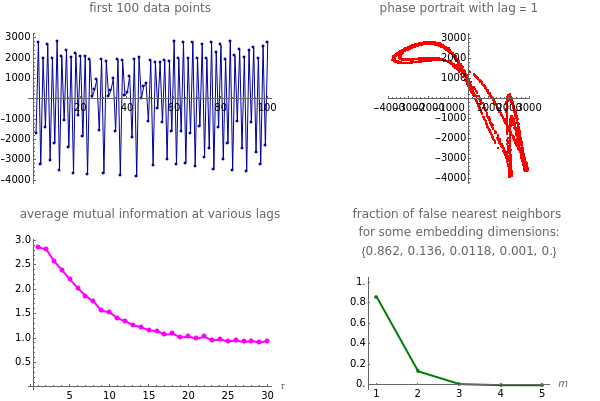
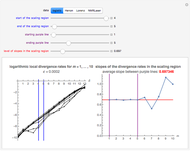
This Demonstration shows how to determine the delay time and embedding dimension for four datasets (each of length 4000). The data is derived from the logistic, Hénon and Lorenz models and NMR laser data. The delay time can be inferred from the average mutual information at various time lags: the suitable delay time is the time lag for which there is a local minimum in the average mutual information. Or, if a local minimum does not exist, the time lag at which the first substantial decrease in the average mutual information has occurred.
[more]
Contributed by: Heikki Ruskeepää (March 2017)
Open content licensed under CC BY-NC-SA
Snapshots
Details
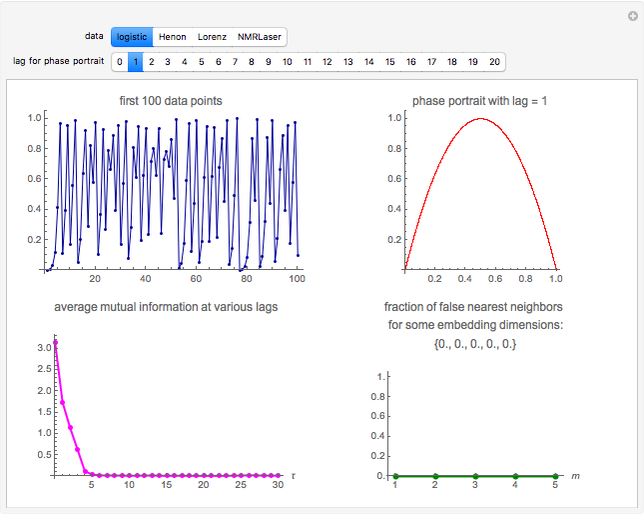
Snapshot 1: Logistic data. The phase portrait unfolds with a time lag of 1, suggesting that the delay time could be 1. The average mutual information does not have a local minimum, but the first substantial decrease stops at time lag 1, suggesting that a suitable delay time could be 1. The fraction of false nearest neighbors drops to zero for embedding dimension 1. In summary, the delay coordinates are simply 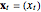 .
.
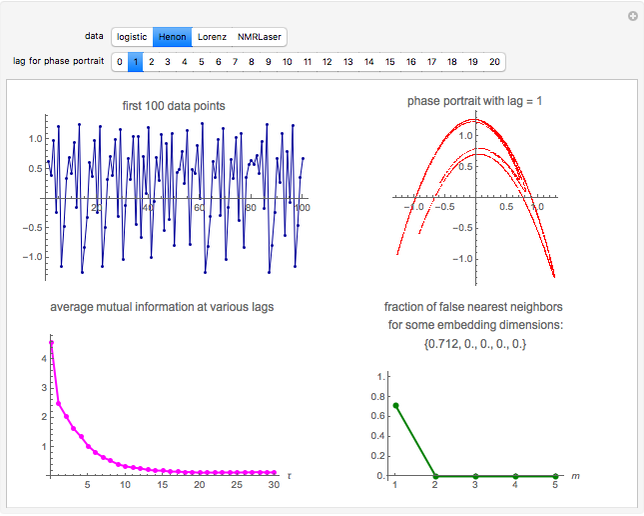
Snapshot 2: Hénon data. The phase portrait unfolds with a time lag of 1, suggesting that the delay time could be 1. The average mutual information does not have a local minimum, but the first substantial decrease stops at time lag 1, suggesting that a suitable delay time could be 1. The fraction of false nearest neighbors drops to zero for embedding dimension 2 (71.2% of nearest neighbors are false for embedding dimension 1). In summary, the delay coordinates are 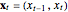 .
.
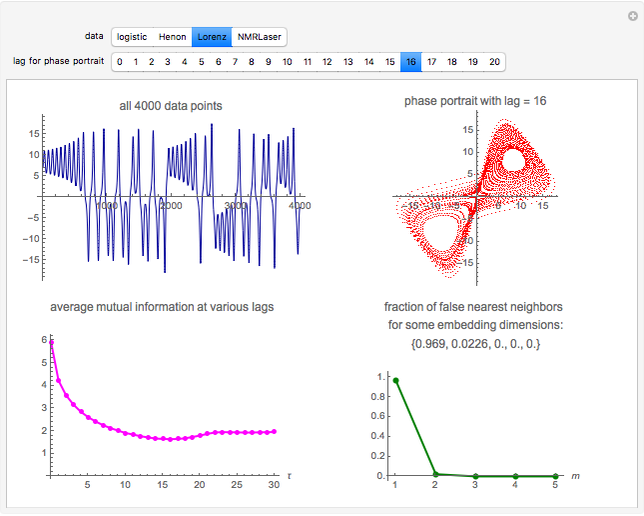
Snapshot 3: Lorenz data. The phase portrait unfolds with a time lag of approximately 16, suggesting that the delay time could be 16. The average mutual information has a local minimum at a time lag of approximately 16, suggesting that a suitable delay time could be 16. The fraction of false nearest neighbors drops to zero for embedding dimension 3 (for embedding dimension 1 it is 96.9%; for embedding dimension 2 it is 2.26%). In summary, the delay coordinates are 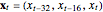 .
.
Snapshot 4: NMR laser data. The phase portrait unfolds with a time lag of 1, suggesting that the delay time could be 1. The average mutual information does not have a clear local minimum, but the first substantial decrease stops at time lag 1, suggesting that a suitable delay time could be 1. The fraction of false nearest neighbors drops to zero for embedding dimension 5 (for embedding dimensions 1, 2, 3 and 4 it is 86.2%, 13.6%, 1.18% and 0.1%, respectively). In summary, the delay coordinates are 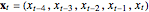 .
.
These four settings are set as bookmarks in the "Bookmarks/Autorun" menu.
Datasets
Each of the four datasets contains 4000 values. The logistic and Hénon datasets are generated from the corresponding difference equation models. These two calculations start with a high enough precision so that even the decimal parts of the last value are all correct (for the logistic and Hénon data, we start with a precision of 2800 and 1200 digits, respectively).
The Lorenz dataset is calculated by sampling from the numerical solution of the three Lorenz differential equations. We have tried to get a high-precision numerical solution by using a working precision of 25, and accuracy and precision goals of 18 (with these settings, we need almost 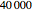 steps).
steps).
For each of these three datasets, 4500 values are actually generated, but the first 500 values are dropped as transient. The NMR laser dataset was earlier available at http://people.maths.ox.ac.uk/mcsharry/lectures/ndc/ndcworkshop.shtml, but appears now to have disappeared. This dataset originally contained 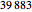 values, but we only use the first 4000 values.
values, but we only use the first 4000 values.
Phase Space Reconstruction
In phase space reconstruction, we have data in the form of a time series 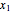 ,
, 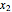 , …, and we choose a delay time
, …, and we choose a delay time  and an embedding dimension
and an embedding dimension 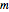 to get
to get 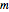 -dimensional delay coordinates
-dimensional delay coordinates 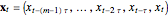 . In this Demonstration, we consider the estimation of the delay time and the embedding dimension.
. In this Demonstration, we consider the estimation of the delay time and the embedding dimension.
Delay Time
There is no rigorous way to determine an optimal value for the delay time, often denoted by  . In practice, the value of
. In practice, the value of  should be such that the values of
should be such that the values of 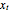 and
and 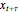 are sufficiently independent to be useful as coordinates in a time-delay vector but not so independent as to have no connection with each other at all. If the signal has a strong (almost) periodic component, a good first guess for the delay time is one-quarter of the period. One of the methods suggested for choosing
are sufficiently independent to be useful as coordinates in a time-delay vector but not so independent as to have no connection with each other at all. If the signal has a strong (almost) periodic component, a good first guess for the delay time is one-quarter of the period. One of the methods suggested for choosing  is the use of mutual information. It measures the general dependence of two variables (recall that autocorrelation, well-known from time series analysis, measures the linear dependence of two variables). In this method, we calculate the average mutual information
is the use of mutual information. It measures the general dependence of two variables (recall that autocorrelation, well-known from time series analysis, measures the linear dependence of two variables). In this method, we calculate the average mutual information 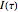 of the variables
of the variables 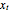 and
and 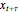 for various values of
for various values of  :
:
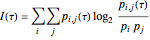 .
.
Here, 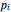 is the relative frequency of the
is the relative frequency of the 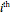 bin of a histogram of the data, that is, the approximate probability that an observation is inside the
bin of a histogram of the data, that is, the approximate probability that an observation is inside the 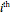 bin. Similarly,
bin. Similarly, 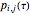 is the approximate probability that
is the approximate probability that 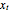 is in the
is in the 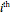 bin and
bin and 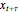 is in the
is in the 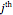 bin. The first minimum of average mutual information marks the delay time
bin. The first minimum of average mutual information marks the delay time  where
where 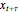 adds maximal information to the knowledge we have from
adds maximal information to the knowledge we have from 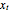 . Accordingly, it is suggested that this value of
. Accordingly, it is suggested that this value of  is used as the delay time in phase space reconstruction.
is used as the delay time in phase space reconstruction.
Embedding Dimension
A widely used method to determine 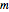 is the method of false nearest neighbors. The idea is that when the embedding dimension is too small, some points of the data are very close to one another, not on the basis of the dynamics, but because the data is projected onto a too low-dimensional space. In the method of false nearest neighbors, we gradually increase the embedding dimension
is the method of false nearest neighbors. The idea is that when the embedding dimension is too small, some points of the data are very close to one another, not on the basis of the dynamics, but because the data is projected onto a too low-dimensional space. In the method of false nearest neighbors, we gradually increase the embedding dimension 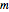 , and for each value of
, and for each value of 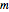 , we search for any false nearest neighbors for each point of the embedded data. This search proceeds as follows.
, we search for any false nearest neighbors for each point of the embedded data. This search proceeds as follows.
When we have increased 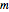 to a value for which we, for the first time, essentially do no not have any more false nearest neighbors, we have identified the correct embedding dimension. For this dimension, the proportion of false nearest neighbors is either essentially zero or very small.
to a value for which we, for the first time, essentially do no not have any more false nearest neighbors, we have identified the correct embedding dimension. For this dimension, the proportion of false nearest neighbors is either essentially zero or very small.
Related Works
For details of analysis of chaotic data with Mathematica, see "Analysis of Chaotic Data with Mathematica" in the Related Links, in which we calculate the correlation dimension and the maximal Lyapunov exponent and also consider prediction for the four datasets.
In the other Demonstrations listed in Related Links, we estimate the correlation dimension and the maximal Lyapunov exponent.
Permanent Citation