Chaotic Data: Maximal Lyapunov Exponent

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
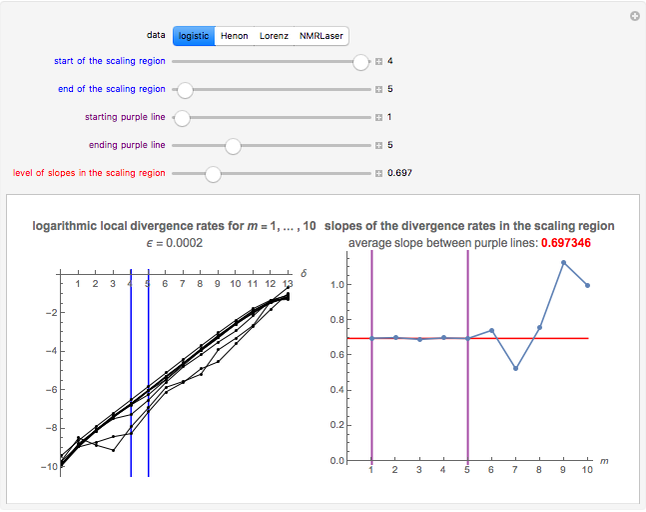
This Demonstration obtains estimates of the maximal Lyapunov exponent for four chaotic datasets (each of length 4000). The data is derived from the logistic, Hénon and Lorenz models and NMR laser data. The figure on the left displays logarithmic divergence rates for some embedding dimensions  (as functions of a time distance
(as functions of a time distance  ). They are calculated at discrete points, which are joined with lines. The logarithmic divergence rates, which require significant computation times, were calculated outside of this Demonstration (for these computations, see "Analysis of Chaotic Data with Mathematica" in the Related Links).
). They are calculated at discrete points, which are joined with lines. The logarithmic divergence rates, which require significant computation times, were calculated outside of this Demonstration (for these computations, see "Analysis of Chaotic Data with Mathematica" in the Related Links).
Contributed by: Heikki Ruskeepää (March 2017)
Open content licensed under CC BY-NC-SA
Snapshots
Details
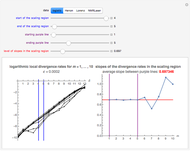
Snapshot 1: Logistic data. The figure on the left shows a narrow scaling region between 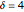 and
and 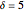 . The slopes of the linear fits for the points between the two blue lines are given in the figure on the right. There, we can see that the slope is approximately 0.697 when the embedding dimension
. The slopes of the linear fits for the points between the two blue lines are given in the figure on the right. There, we can see that the slope is approximately 0.697 when the embedding dimension 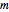 has values from 1 to 5. The value 0.697 is our estimate of the maximal Lyapunov exponent. The actual value of the maximal Lyapunov exponent for the logistic model is
has values from 1 to 5. The value 0.697 is our estimate of the maximal Lyapunov exponent. The actual value of the maximal Lyapunov exponent for the logistic model is 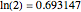 [1, p. 417]. Our estimate is close to the actual value.
[1, p. 417]. Our estimate is close to the actual value.
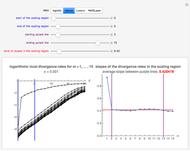
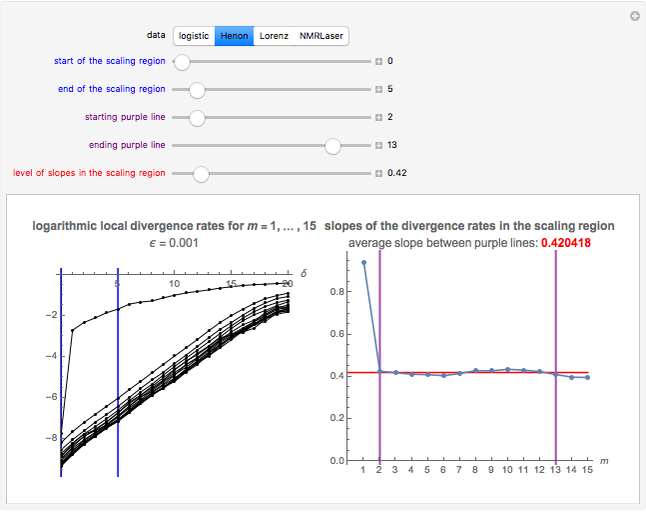
Snapshot 2: Hénon data. A scaling region seems to be between  and
and 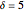 . The slopes of linear fits of these points are approximately 0.420 for
. The slopes of linear fits of these points are approximately 0.420 for 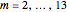 . The value 0.420 is the estimate of the maximal Lyapunov exponent. The actual value of the maximal Lyapunov exponent for the Hénon model is 0.41922 [1, p. 421]. Our estimate of 0.420 is close to the actual value.
. The value 0.420 is the estimate of the maximal Lyapunov exponent. The actual value of the maximal Lyapunov exponent for the Hénon model is 0.41922 [1, p. 421]. Our estimate of 0.420 is close to the actual value.
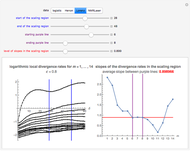
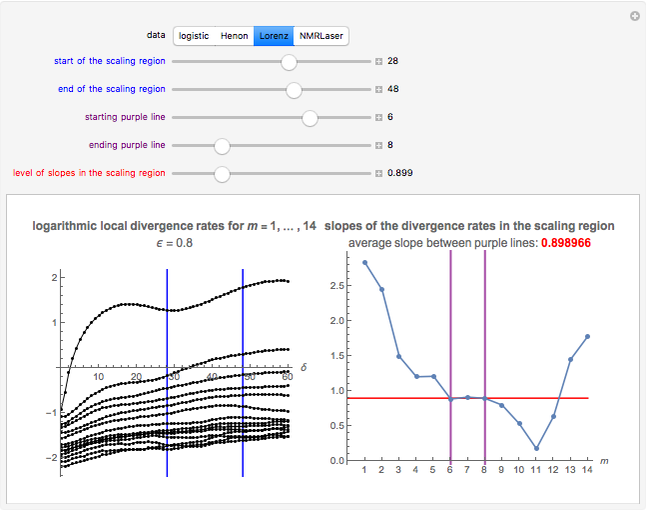
Snapshot 3: Lorenz data. A scaling region seems to be between 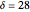 and
and 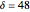 . The slopes of linear fits of these points are approximately 0.899 for
. The slopes of linear fits of these points are approximately 0.899 for 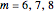 . The value 0.899 is the estimate of the maximal Lyapunov exponent. The maximal Lyapunov exponent of the original continuous Lorenz system is 0.9056 [1, p. 431]. Our estimate of 0.899 based on the sampled Lorenz system is close to the actual value.
. The value 0.899 is the estimate of the maximal Lyapunov exponent. The maximal Lyapunov exponent of the original continuous Lorenz system is 0.9056 [1, p. 431]. Our estimate of 0.899 based on the sampled Lorenz system is close to the actual value.
Snapshot 4: NMR laser data. A scaling region seems to be between  and
and 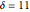 . The slopes of linear fits of these points are approximately 0.276 for
. The slopes of linear fits of these points are approximately 0.276 for  . The value 0.276 is the estimate of the maximal Lyapunov exponent.
. The value 0.276 is the estimate of the maximal Lyapunov exponent.
These four settings are set as bookmarks in the "Bookmarks/Autorun" menu.
Maximal Lyapunov Exponent
The maximal Lyapunov exponent is a characteristic of the dynamical system and quantifies the magnitude of chaos. Indeed, in chaotic systems, nearby trajectories diverge exponentially fast. The properly averaged exponent of this divergence is the maximal Lyapunov exponent. It describes the average rate at which predictability of the system is lost.
The maximal Lyapunov exponent can be estimated with the method of local divergence rates, as follows. Prepare the 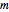 -dimensional delay coordinates
-dimensional delay coordinates 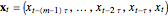 . Fix an integer
. Fix an integer  and choose a
and choose a  from the set
from the set 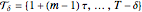 . Then find all points
. Then find all points  that are in an
that are in an  -neighborhood of
-neighborhood of  ; let
; let 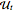 be the set of these indices
be the set of these indices 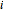 . For these
. For these 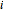 , calculate the distance
, calculate the distance 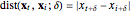 between
between  and
and  after the relative time
after the relative time  . Local divergence rates are then calculated from
. Local divergence rates are then calculated from
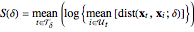 .
.
Program for Local divergence Rates
The logarithmic divergence rates were calculated outside of this Demonstration. They can be calculated with the following program:
S[data_, τ_, mMax_, ϵ_, δMax_, h_] := {ϵ, h,
ParallelTable[Module[{emb, nn, nf, neigh},
emb = Table[Take[data, {i, i + τ (m - 1), τ}], {i, Length[data] - τ (m - 1)}];
nn = Length[emb];
nf = Nearest[emb -> Range[nn]];
neigh = Table[DeleteCases[Rest[nf[emb[[t]], {∞, ϵ}]], p_ /; p > nn - δMax], {t, nn - δMax}];
Table[{δ, Mean[DeleteCases[
Table[If[Length[neigh[[t]]] == 0, "d",
Log[Mean[Abs[data[[t + (m - 1) τ + δ]] - data[[neigh[[t]] + (m - 1) τ + δ]]]]]],
{t, nn - δMax}], "d"|Indeterminate]]},
{δ, 0, δMax}]],
{m, mMax}]}
Here are the suitable commands to calculate the logarithmic divergence rates for the four datasets:
logistic = S[data, 1, 10, 0.0002, 13, 1]
Hénon = S[data, 1, 15, 0.001, 20, 1]
Lorenz = S[data, 16, 14, 0.8, 60, 0.01]
NMRLaser = S[data, 1, 14, 150.0, 15, 1]
A typical computing time is from a few seconds to half a minute.
We used the same four datasets (each containing 4000 values) as in "Chaotic Data: Delay Time and Embedding Dimension"; see Related Links. For each dataset, we also used here the value of the delay time  that we obtained in that Demonstration (these delay times are 1, 1, 16 and 1 for the four datasets, respectively).
that we obtained in that Demonstration (these delay times are 1, 1, 16 and 1 for the four datasets, respectively).
Related Work
For details and other references, see "Analysis of Chaotic Data with Mathematica" in the Related Links. In that work, we estimate the delay time, embedding dimension and correlation dimension, and also consider prediction.
In the Demonstration Chaotic Data: Delay Time and Embedding Dimension, we estimate the delay time and embedding dimension for the same four datasets. In the Demonstration Chaotic Data: Correlation Dimension, we estimate the correlation dimension.
Reference
[1] J. C. Sprott, Chaos and Time-Series Analysis, Oxford, UK: Oxford University Press, 2003.
Permanent Citation