Chemical Reaction in a Non-Newtonian Fluid

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
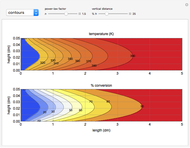
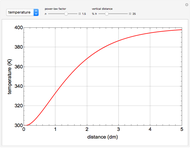
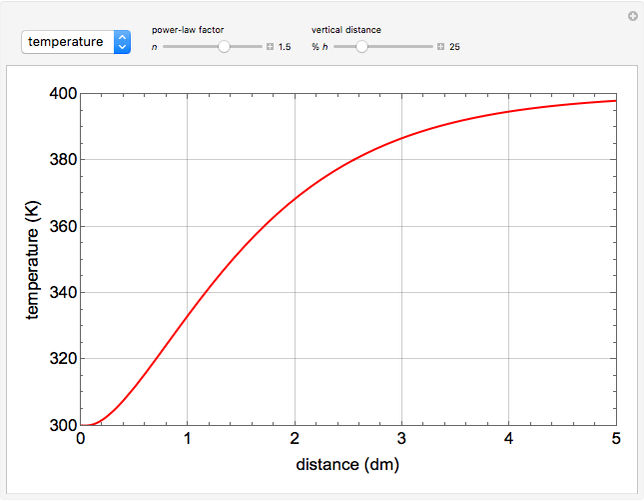
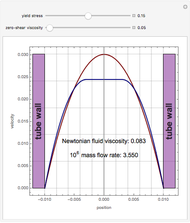
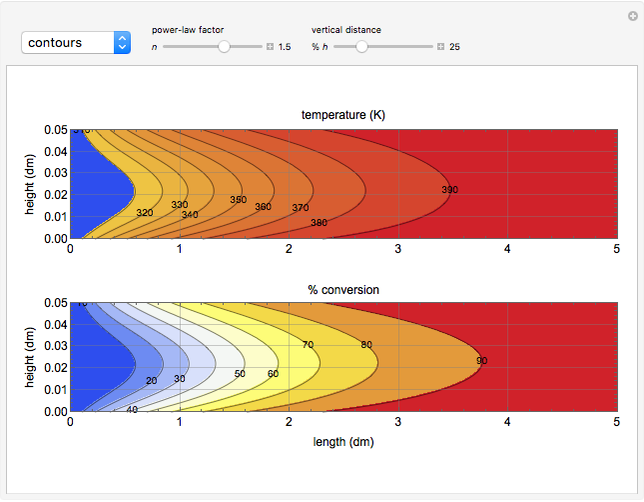
This Demonstration illustrates a variation of the Graetz problem [1]. A chemical reaction 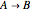 takes place in a non-Newtonian power-law fluid that is in laminar flow in the channel between two parallel plates. In the inlet region
takes place in a non-Newtonian power-law fluid that is in laminar flow in the channel between two parallel plates. In the inlet region  , the fluid temperature
, the fluid temperature 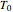 and the concentration
and the concentration 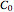 of component
of component 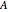 are uniform; in the region
are uniform; in the region  , the wall temperature
, the wall temperature 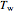 and the concentration
and the concentration  of component
of component 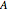 are maintained constant.
are maintained constant.
Contributed by: Clay Gruesbeck (September 2018)
Open content licensed under CC BY-NC-SA
Details
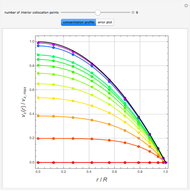
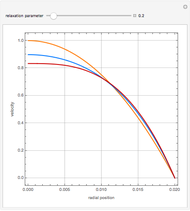
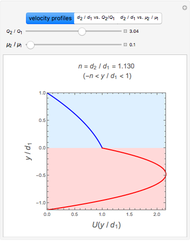
The laminar velocity profile of a power-law fluid is given by [1]
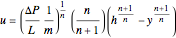
where  and
and 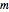 are power-law parameters,
are power-law parameters,  is the distance between the parallel plates,
is the distance between the parallel plates,  is the vertical coordinate and
is the vertical coordinate and  is the horizontal pressure gradient.
is the horizontal pressure gradient.
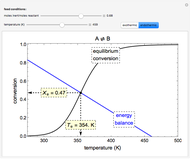
The energy and mass conservation equations, assuming that all physical properties are constant and that viscous dissipation and axial heat conduction effects are negligible, are:
 ,
,
with
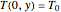 ,
,
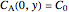 ,
,
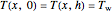
and
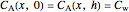 .
.
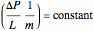 ,
,
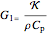 ,
,
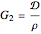 ,
,
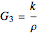 .
.
The results show that the temperature and conversion profiles are parabolic and become progressively blunter as the value of  decreases below unity and sharper for
decreases below unity and sharper for 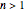 .
.
Reference
[1] R. B. Bird, W. E. Stewart and E. N. Lightfoot, Transport Phenomena, 2nd ed., New York: John Wiley & Sons, Inc., 2002.
Snapshots
Permanent Citation