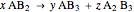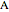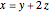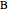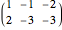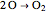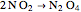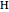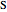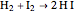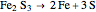Chemical Reactions Represented on a 2D Simplex

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
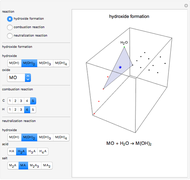
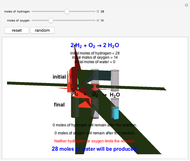
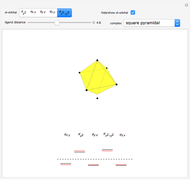
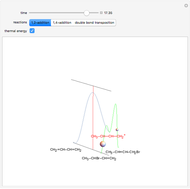
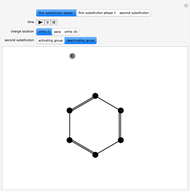
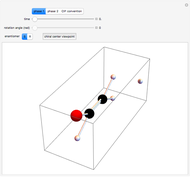
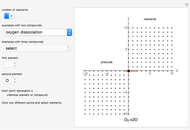
This Demonstration shows the connection between the equation for a balanced chemical reaction and its geometrical representation by a simplex: the figure formed from  vertices in a space of
vertices in a space of  dimensions, where
dimensions, where  is the number of chemical elements involved in the reaction. In two-dimensional space the simplex is a triangle, while in three-dimensional space it is a tetrahedron.
is the number of chemical elements involved in the reaction. In two-dimensional space the simplex is a triangle, while in three-dimensional space it is a tetrahedron.
Contributed by: D. Meliga and S. Z. Lavagnino (April 2017)
With additional contributions by: A. Chiavassa and G. Follo
Open content licensed under CC BY-NC-SA
Snapshots
Details
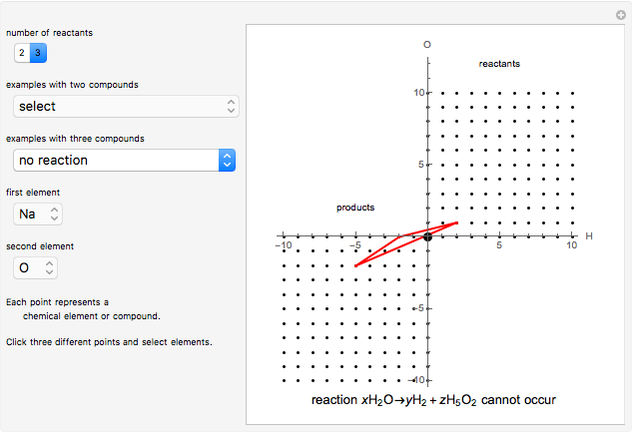
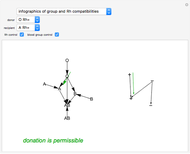
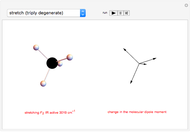
As a graphical representation, we choose the subscripts of reactants as positive and the subscripts of products as negative; for this reason, points all fall in the first and third quadrants. Click on the selected points. Each axis represents an element, which can be selected from the popup menus "first element" and "second element." A large selection of elements is given; boron and other nonmetals are marked in red.
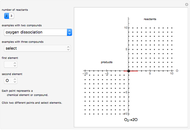
Snapshot 1: with "number of compounds" set to 2, the oxygen dissociation reaction ( ) is possible because the 1-simplex passes through the origin
) is possible because the 1-simplex passes through the origin
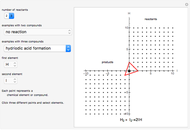
Snapshot 2: with "number of compounds" set to 3, the hydriodic acid reaction (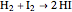 ) is possible because the origin is inside the 2-simplex represented by the triangle
) is possible because the origin is inside the 2-simplex represented by the triangle
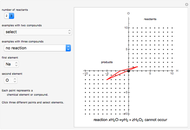
Snapshot 3: with "number of compounds" set to 3, a reaction does not occur because the origin is not inside the 2-simplex
Reference
[1] G. Follo and S. Z. Lavagnino "Bilanciamento delle Reazioni Chimiche e Sistemi Lineari," La Chimica nela Scuola, Anno XXXIII, n. 1, 2011 pp. 18–26. www.soc.chim.it/sites/default/files/cns/pdf/2011-1.pdf.
Permanent Citation