Choosing Initial Parameter Values for Nonlinear Regression

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
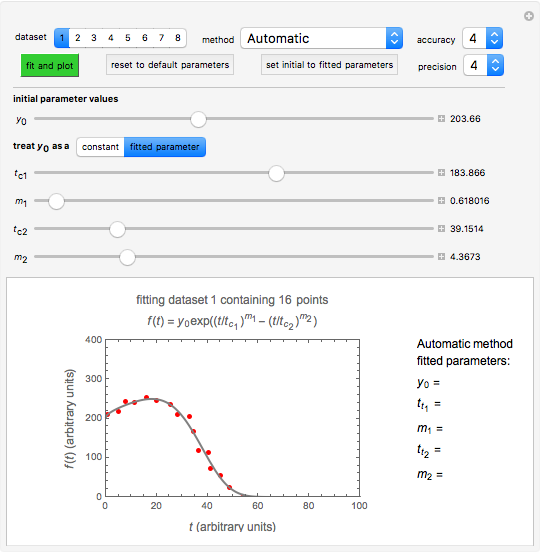
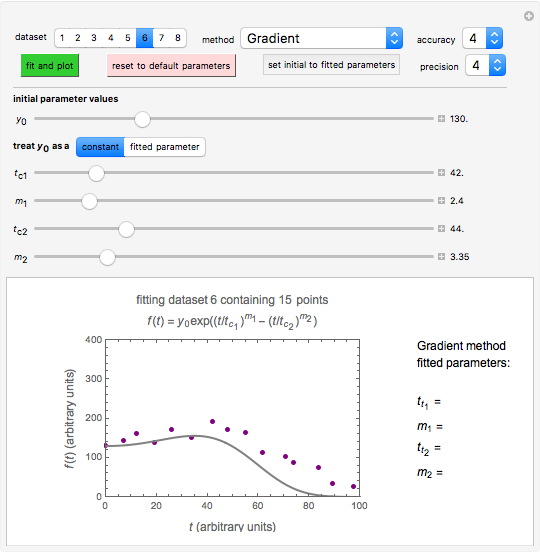
Fitting scattered experimental data with a multi-parameter model by nonlinear regression is frequently hampered by the difficulty in making sufficiently good guesses of the parameters' initial values. This Demonstration lets you plot the points from one of eight datasets and then use the model to generate a curve that approximately matches the data by manually adjusting the parameters’ values with sliders. The values that produce the visually matched curve are then used as the initial guesses to the regression procedure. The method is demonstrated with different scattered peaked datasets to be fitted with a double-stretched exponential model having four or five adjustable parameters. Hints: Start by matching 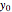 first. Try the Gradient method if Automatic frequently fails.
first. Try the Gradient method if Automatic frequently fails.
Contributed by: Mark D. Normand, Murray Eisenberg, and Micha Peleg (May 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
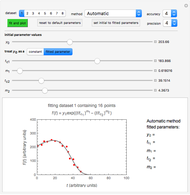
Snapshot 1: dataset 1 and corresponding curve after manually adjusting the parameters for successful completion of the regression using the Automatic method (five-parameter model where 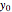 is to be fitted)
is to be fitted)
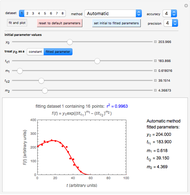
Snapshot 2: dataset 1 and corresponding curve after successful completion of the regression using the Automatic method (five-parameter model where 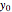 is to be fitted)
is to be fitted)
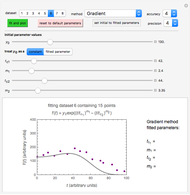
Snapshot 3: dataset 6 and corresponding curve after manually adjusting the parameters resulting in unsuccessful completion of the regression using the Gradient method (four-parameter model where 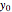 is fixed)
is fixed)
Snapshot 4: dataset 6 and corresponding curve after manually adjusting the parameters for successful completion of the regression using the Gradient method (four-parameter model where 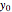 is fixed)
is fixed)
Snapshot 5: dataset 6 and corresponding curve after successful completion of the regression using the Gradient method (four-parameter model where 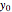 is fixed)
is fixed)
This Demonstration shows how scattered peaked data can be successfully fitted by nonlinear regression by finding initial guesses close enough to the parameters' actual values to yield a successful fit. You may choose any one of eight datasets and then attempt to match its plotted points with a curve using the model parameters’ sliders. The fitting model serving as an example is in the form of a double-stretched exponential  where
where 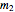 >
>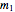 . A setter bar is first used to choose between a four-parameter version of the model where
. A setter bar is first used to choose between a four-parameter version of the model where 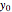 is fixed as a constant and
is fixed as a constant and 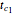 ,
, 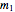 ,
, 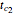 , and
, and 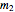 are adjustable parameters, and a five-parameter version where
are adjustable parameters, and a five-parameter version where 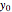 is also an adjustable parameter.
is also an adjustable parameter.
To start the procedure, select a dataset and click the "fit and plot" button. With the method set to Automatic the regression will fail with the default parameter values, and the message "Fit failed!" will be displayed in red above the plot. By adjusting the parameters’ sliders—always start by moving the 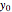 slider until the curve passes through the first data point—try to match the curve to the data points and click on the "fit and plot" button again until successful, in which case the regression correlation coefficient,
slider until the curve passes through the first data point—try to match the curve to the data points and click on the "fit and plot" button again until successful, in which case the regression correlation coefficient, 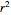 , will be displayed in blue above the plot and the fitted parameter values will be shown to its left. Another option after failure is to change the method to Gradient. For these models and data sets the Gradient method is more likely to give a successful fit than Automatic. If both methods yield a successful fit, you should prefer the one giving the highest
, will be displayed in blue above the plot and the fitted parameter values will be shown to its left. Another option after failure is to change the method to Gradient. For these models and data sets the Gradient method is more likely to give a successful fit than Automatic. If both methods yield a successful fit, you should prefer the one giving the highest 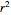 value. Additional controls let you change the regression's AccuracyGoal and PrecisionGoal.
value. Additional controls let you change the regression's AccuracyGoal and PrecisionGoal.
After a successful fit, changing any control will erase the displayed 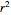 and parameter values and signal that you are ready for a new fit attempt using the current slider settings as the parameters' initial values. To set the parameter sliders to the most recently fitted values, click the "set initial to fitted parameters" button. Click the "reset to default parameters" button to return the sliders to the original default parameter values.
and parameter values and signal that you are ready for a new fit attempt using the current slider settings as the parameters' initial values. To set the parameter sliders to the most recently fitted values, click the "set initial to fitted parameters" button. Click the "reset to default parameters" button to return the sliders to the original default parameter values.
An example of using this procedure with real experimental data can be found in [1].
Reference
[1] M. G. Corradini, M. D. Normand, M. Eisenberg, and M. Peleg, "Evaluation of a Stochastic Inactivation Model for Heat-Activated Spores of Bacillus spp.," Applied & Environmental Microbiology, 76, 2010 pp. 4402–4412.
Permanent Citation