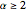Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Classical Particle in a Coulomb-Like Radial Potential

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

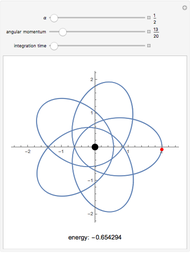
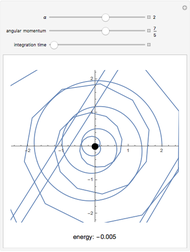
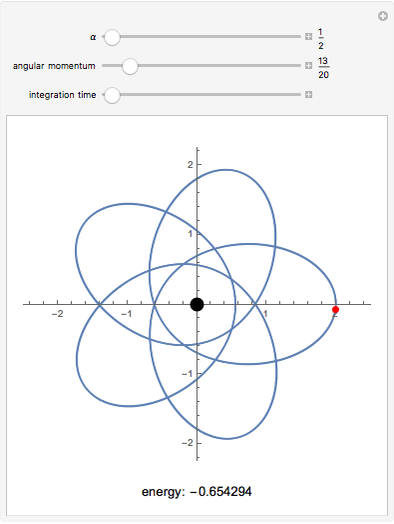
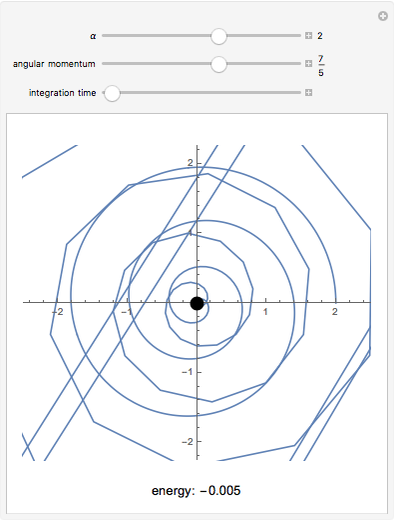
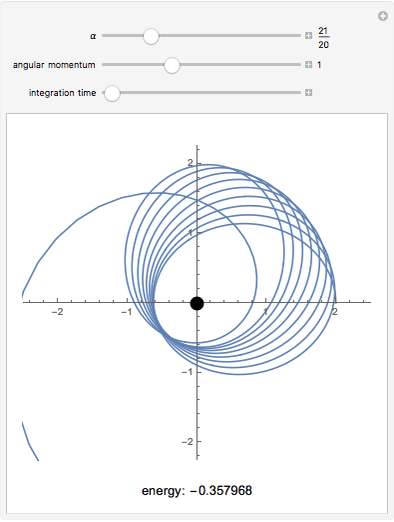
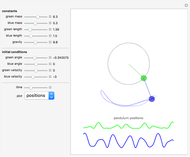
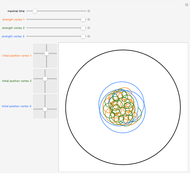
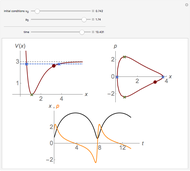
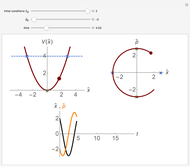
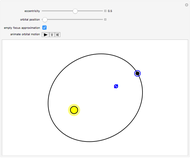
This Demonstration shows the negative energy trajectories of a point mass moving in the radially symmetric potential 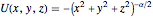. Due to the radial symmetry the point mass moves in a two-dimensional plane perpendicular to the angular momentum vector.

[more]

The case of corresponds to the Coulomb potential, where negative energy trajectories are periodic. For , all the negative energy trajectories go through the origin.

[less]

Contributed by: Oleksandr Pavlyk (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

All physical values displayed have been made to be dimensionless.

The initial velocity of the moving point mass is perpendicular to the radius.

Newton's equations of motion in polar coordinates read:

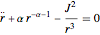and ,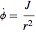

where 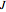is the angular momentum.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send