Clausius-Clapeyron Equation for Some Common Liquids

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
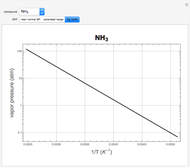
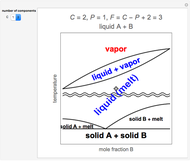
The Clausius–Clapeyron equation determines the vapor pressure 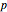 of a liquid as a function of temperature
of a liquid as a function of temperature  (in degrees K). In differential form, the CC equation can be written
(in degrees K). In differential form, the CC equation can be written  , where
, where  is the standard molar enthalpy of vaporization. If the enthalpy of vaporization is assumed constant over a temperature range, the equation can be integrated to give
is the standard molar enthalpy of vaporization. If the enthalpy of vaporization is assumed constant over a temperature range, the equation can be integrated to give 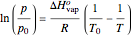 . For
. For 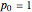 atm,
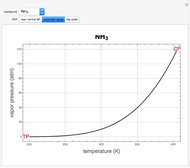
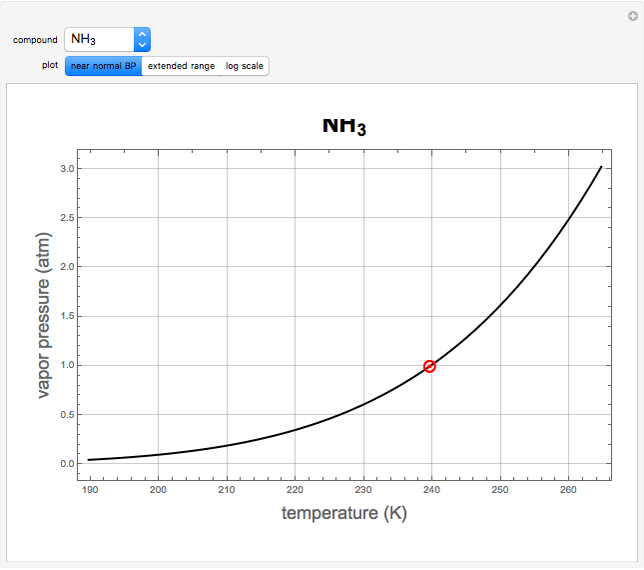
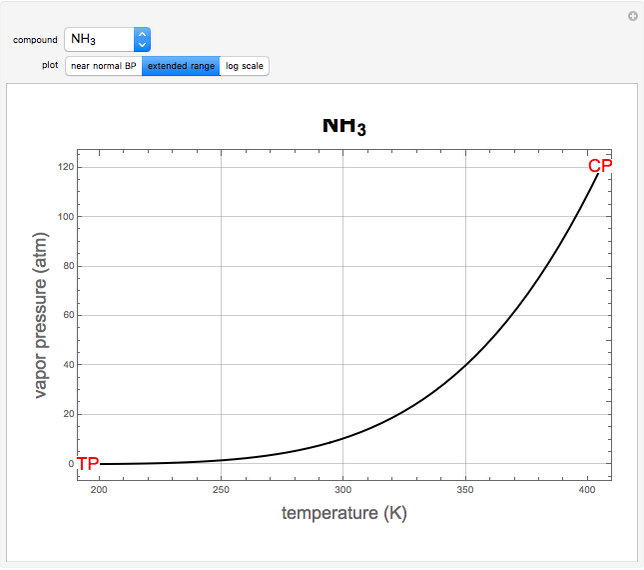
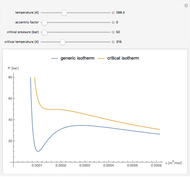
atm,  is the normal boiling point. Data for 20 common gases is tabulated. The first set of plots, in the vicinity of the normal boiling point (marked by a red circle), is likely to be quite accurate. Vapor pressure data for each compound is also tabulated over an extended range of temperatures, from the triple point (TP) to the critical point (CP). Results farther removed from the normal BP are likely to be less dependable. Improved accuracy can be obtained using the Antoine equation
is the normal boiling point. Data for 20 common gases is tabulated. The first set of plots, in the vicinity of the normal boiling point (marked by a red circle), is likely to be quite accurate. Vapor pressure data for each compound is also tabulated over an extended range of temperatures, from the triple point (TP) to the critical point (CP). Results farther removed from the normal BP are likely to be less dependable. Improved accuracy can be obtained using the Antoine equation  , where
, where  ,
, 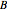 ,
,  are empirical constants for each substance.
are empirical constants for each substance.
Contributed by: S. M. Blinder (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Reference: any standard physical chemistry text.
Permanent Citation