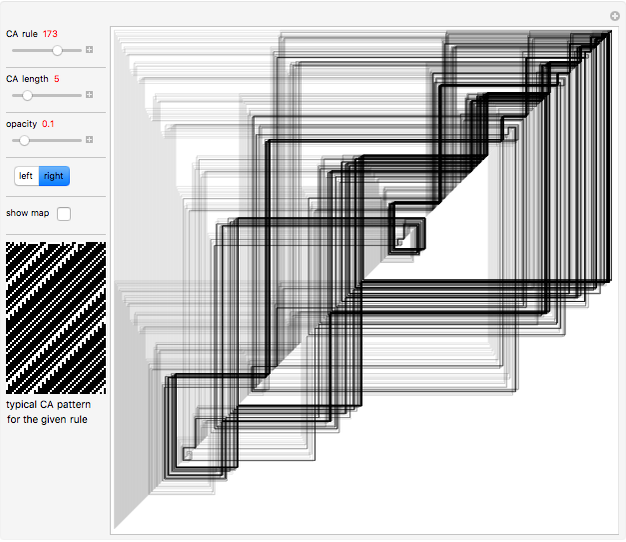
Cobweb Diagrams of Elementary Cellular Automata

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
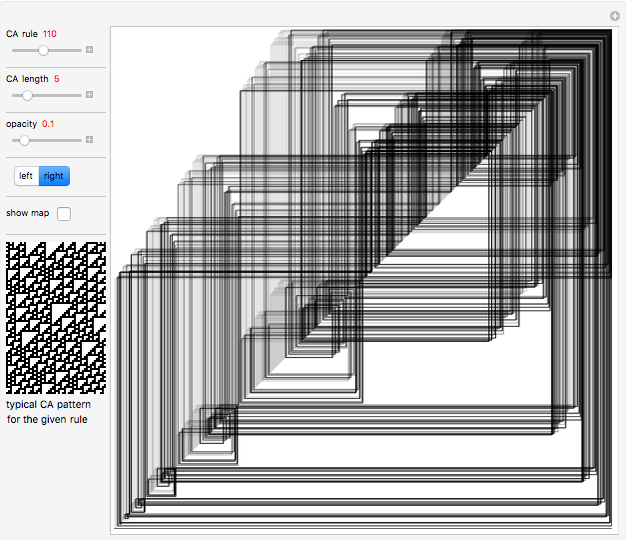
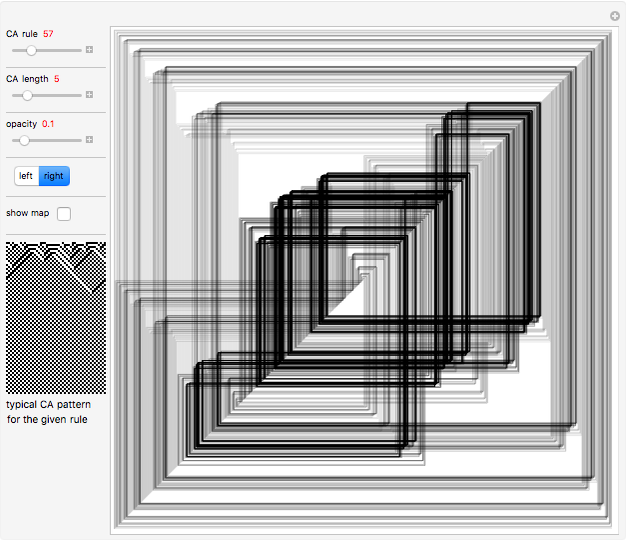
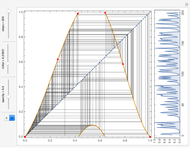
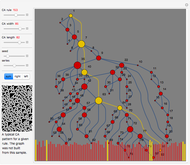
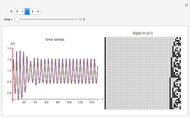
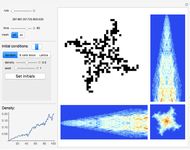
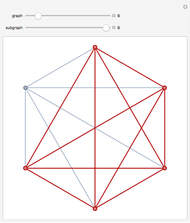
Each possible state in the evolution of an elementary cellular automaton (ECA) can be uniquely labeled by an integer. For a finite-width ECA, this set is mapped to itself during the ECA evolution. Thus an ECA defines a recurrence relation on a finite set of integers. In fact, this can be applied to map the Cantor set to itself (see Related Links and Details sections).
[more]
Contributed by: Vitaliy Kaurov (April 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
References
[1] J. D. Farmer, "Dimension, Fractal Measures, and Chaotic Dynamics," in Evolution of Order and Chaos in Physics, Chemistry, and Biology: Proceedings of the International Symposium on Synergetics, Bavaria, Germany (H. Haken, ed.), Berlin: Springer-Verlag, 1982 pp. 228–246. doi:10.1007/978-3-642-68808-9_20.
[2] J. D. Farmer, "Information Dimension and the Probabilistic Structure of Chaos," Zeitschrift für Naturforschung A, 37, 1982 pp. 1304–1325.
Permanent Citation
"Cobweb Diagrams of Elementary Cellular Automata"
http://demonstrations.wolfram.com/CobwebDiagramsOfElementaryCellularAutomata/
Wolfram Demonstrations Project
Published: April 18 2013