Coexistence of Qubit Effects

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
Suppose two qubit measurements are given by the effects 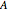 and
and 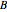 , which are parametrized by values of bias
, which are parametrized by values of bias  and
and 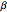 and sharpness
and sharpness  and
and  , which are the lengths of the corresponding vectors
, which are the lengths of the corresponding vectors  and
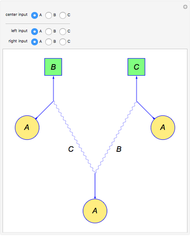
and  that give the directions along which the measurements are performed. The projection of
that give the directions along which the measurements are performed. The projection of  onto
onto  is labeled as
is labeled as  (
( axis) and the orthogonal complement is labeled as
axis) and the orthogonal complement is labeled as  (
(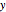 axis). For given
axis). For given  ,
, 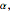 and
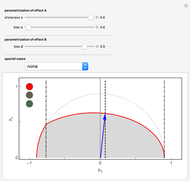
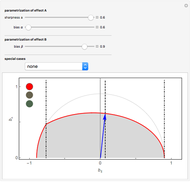
and 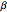 , the graph shows the area for possible choices of such
, the graph shows the area for possible choices of such  for which the effects
for which the effects 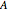 and
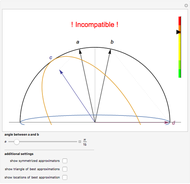
and 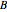 are simultaneously measurable, that is, coexistent (the area shaded gray bounded by the thick red curve). The thin black circle represents the condition for
are simultaneously measurable, that is, coexistent (the area shaded gray bounded by the thick red curve). The thin black circle represents the condition for 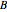 to be an effect (a valid measurement). The dot-dashed lines (if present) define the region within which there is a nontrivial restriction on the vector
to be an effect (a valid measurement). The dot-dashed lines (if present) define the region within which there is a nontrivial restriction on the vector  , in which case either an orange or a red light shines, as opposed to a green light, which corresponds to unrestricted joint measurability. A dashed line, together with the blue vector, shows the strictest limitation on
, in which case either an orange or a red light shines, as opposed to a green light, which corresponds to unrestricted joint measurability. A dashed line, together with the blue vector, shows the strictest limitation on  for the chosen parameters—for all
for the chosen parameters—for all  such that they are not longer than the blue vector, there is no angle restriction.
such that they are not longer than the blue vector, there is no angle restriction.
Contributed by: Peter Stano, Daniel Reitzner, and Teiko Heinosaari (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
A spin 1/2 state can be represented by a vector (arrow) of length one in three-dimensional space. However, this analogy is imperfect, because the quantum state has some peculiar properties that a "traditional" arrow does not have. For example, it is impossible to measure simultaneously projections of the arrow along two different axes—only one such measurement at a time is allowed in principle. What we are about to present are possible pairs of joint measurements on a spin 1/2 particle—given not only by projections, but by Positive Operator Valued Measures (POVMs)—which are allowed by quantum mechanics.
Like a state, a two-outcome measurement on a qubit (uniquely determined by effect 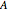 ) can be represented by an arrow, with two additional characteristics describing possible measurement noise (errors): the length
) can be represented by an arrow, with two additional characteristics describing possible measurement noise (errors): the length  is the fuzziness of the measurement—the smaller the length, the more probable it is that after the measurement we declare a state to be pointing along
is the fuzziness of the measurement—the smaller the length, the more probable it is that after the measurement we declare a state to be pointing along  even when it, in fact, points in the opposite direction. The second characteristic is the so-called bias
even when it, in fact, points in the opposite direction. The second characteristic is the so-called bias  , for which the larger the distance is from 1, the more we are biased toward declaring the state to be pointing in one of the directions given by the vector
, for which the larger the distance is from 1, the more we are biased toward declaring the state to be pointing in one of the directions given by the vector  .
.
Given a measurement (effect) 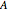 that measures the projection of the state along the
that measures the projection of the state along the  axis with unsharpness
axis with unsharpness  and bias
and bias  , the area shaded gray shows the possible vectors
, the area shaded gray shows the possible vectors  for a fixed bias
for a fixed bias 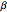 . The border of the allowed area consists of two parts: one is a part of a circle (standing for the condition on
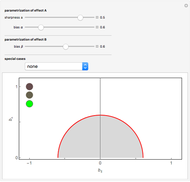
. The border of the allowed area consists of two parts: one is a part of a circle (standing for the condition on 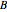 to be an effect, a physically feasible measurement) and the other one a fourth-order curve (in the graphic, these two parts are delimited by dot-dashed lines). If there is only a circle, the measurement
to be an effect, a physically feasible measurement) and the other one a fourth-order curve (in the graphic, these two parts are delimited by dot-dashed lines). If there is only a circle, the measurement 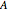 is so noisy that any measurement
is so noisy that any measurement 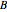 is allowed by quantum mechanics and the green light is on (the first special case, snapshot 2). If the yellow light is on, there exists a nontrivial restriction on possible measurements
is allowed by quantum mechanics and the green light is on (the first special case, snapshot 2). If the yellow light is on, there exists a nontrivial restriction on possible measurements 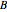 , and it is hardest to measure in the direction perpendicular to
, and it is hardest to measure in the direction perpendicular to  (the shortest possible arrow for
(the shortest possible arrow for 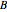 is along the
is along the 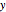 axis; see the third special case, snapshot 3). If the red light is on, not only is the restriction present, but it is asymmetric with respect to the
axis; see the third special case, snapshot 3). If the red light is on, not only is the restriction present, but it is asymmetric with respect to the 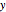 axis (the second and fourth special cases, snapshot 1 and the thumbnail).
axis (the second and fourth special cases, snapshot 1 and the thumbnail).
This solution to a long-standing problem in quantum mechanics was solved in: P. Stano, D. Reitzner, and T. Heinosaari, "Coexistence of Qubit Effects," Phys. Rev. A 78, 012315, 2008, where the four special cases are also discussed in more detail.
Other papers that are concerned with this topic are:
P. Busch and H.-J. Schmidt, "Coexistence of Qubit Effects," arXiv:0802.4167v3, 2008.
S. Yu, N. Liu, L. Li, and C. H. Oh, "Joint Measurement of Two Unsharp Observables of a Qubit," arXiv:0805.1538v2, 2008.
Permanent Citation