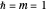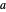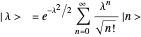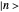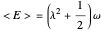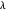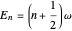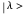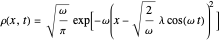Coherent States of the Harmonic Oscillator

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
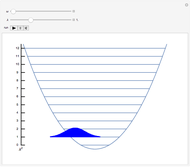
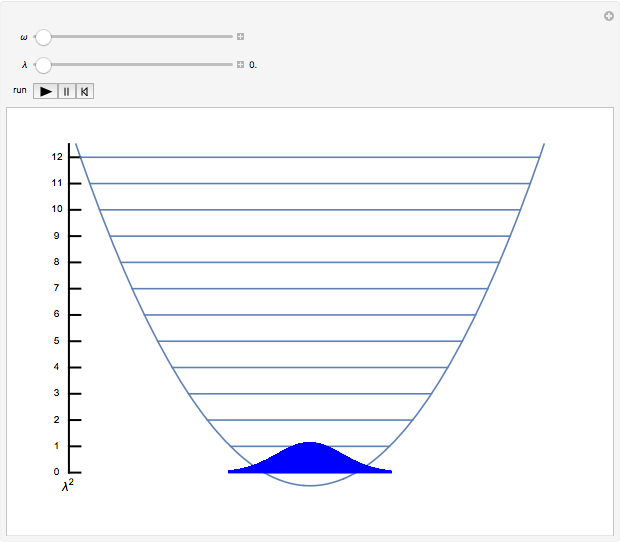
Coherent states of a harmonic oscillator are wavepackets that have the shape of the ground state probability distribution but undergo the motion of a classical oscillator of arbitrary energy. Schrödinger first considered these in the context of minimum-uncertainty wavepackets. More recently (1963), Roy Glauber exploited coherent states in quantum-mechanical descriptions of oscillating electromagnetic fields in quantum optics and in connection with the Hanbury-Brown and Twiss experiment. Glauber shared the 2005 Nobel Prize in Physics for this work.
[more]
Contributed by: S. M. Blinder (March 2011)
With contribution by Jeremy Michelson
Open content licensed under CC BY-NC-SA
Snapshots
Details
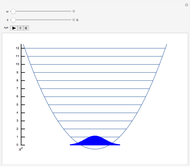
Snapshot 1:  wavepacket
wavepacket
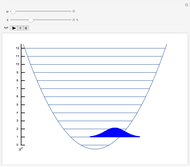
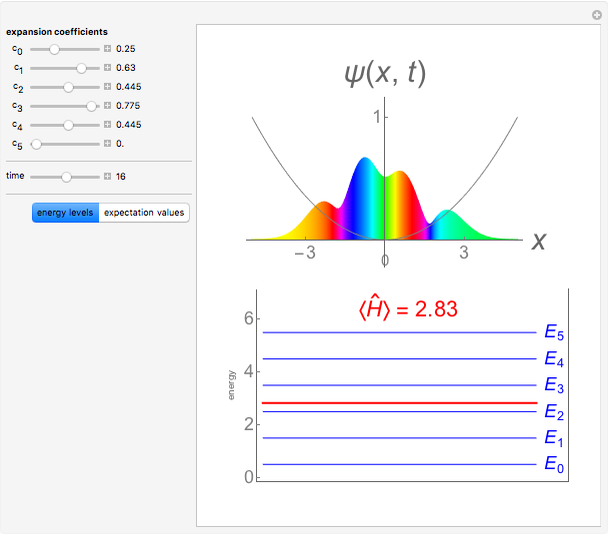
Snapshots 2,3: oscillation of 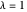 wavepacket
wavepacket
Permanent Citation