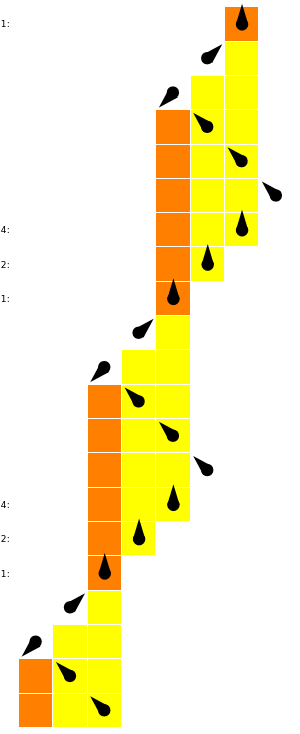
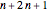Collatz Sequence Computed by a Turing Machine
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
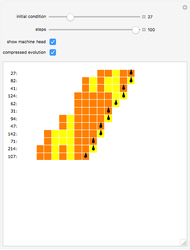
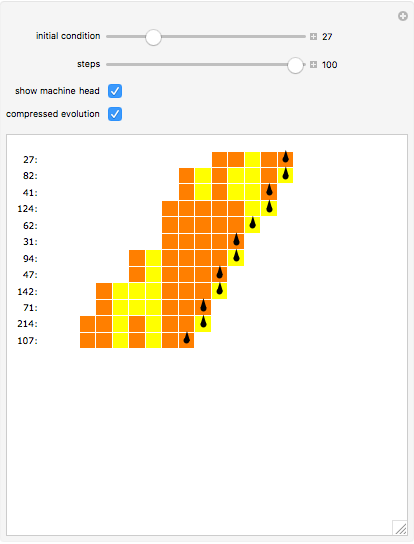
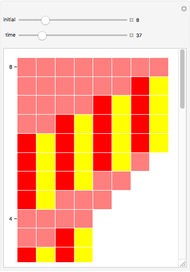
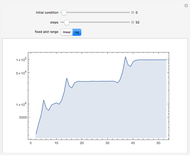
The Collatz sequence is formed by an iteration of numbers produced by the following rule: If  is even, then replace
is even, then replace  by
by 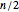 ; if
; if  is odd then replace
is odd then replace  by
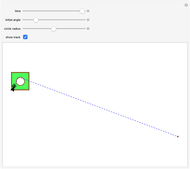
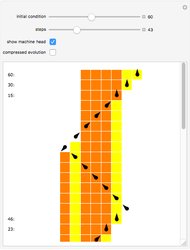
by 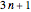 . This Demonstration implements an 8-state 3-color Turing machine that computes this sequence.
. This Demonstration implements an 8-state 3-color Turing machine that computes this sequence.
Contributed by: Emmanuel Garces Medina (October 2011)
Open content licensed under CC BY-NC-SA
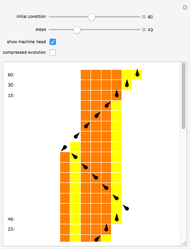
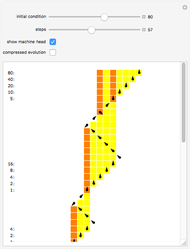
Snapshots
Details
Permanent Citation