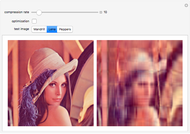
Color Image Compression via the Higher-Order Singular Value Decomposition (HOSVD)

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
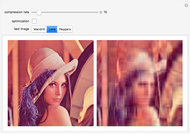
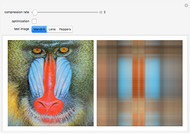
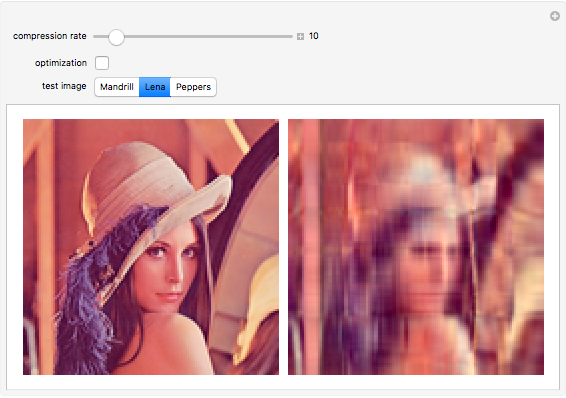
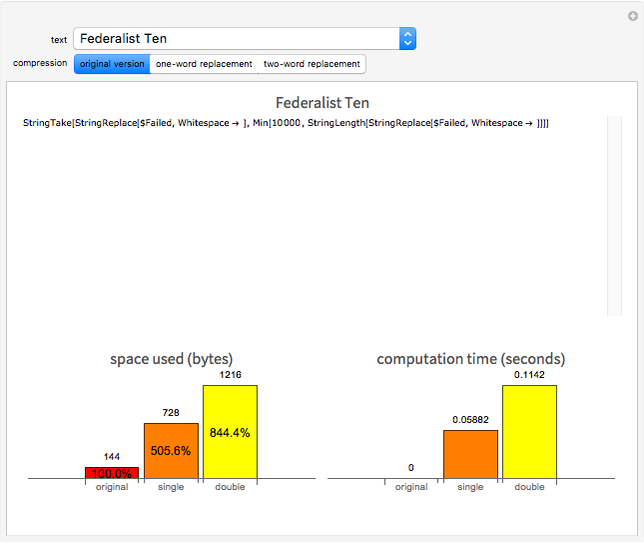
This Demonstration shows a method for data compression via the higher-order singular value decomposition (HOSVD) with color images interpreted as third-order tensors. The data compression is achieved by decreasing the tensor ranks in the 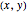 pixel dimensions, while the third dimension (RGB channels) is not changed.
pixel dimensions, while the third dimension (RGB channels) is not changed.
Contributed by: Michael Weyrauch and Alexander Scholz (June 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Higher-order singular value decomposition (HOSVD) is a generalization of the well-known singular value decomposition (SVD) for matrices. HOSVD defines a decomposition for tensors of higher dimension (greater than two). This decomposition enables reducing the rank of the tensors, which can be used as a method for data compression. In this Demonstration, color images are interpreted as third-order tensors. The third dimension corresponds to RGB channels and is not rank reduced. You can vary the ranks of the first and second dimensions, the 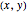 pixels.
pixels.
For a matrix, the column and row ranks are equal, and a unique matrix rank can be defined. For higher-dimensional tensors this does not hold, but a rank for each of its dimensions can be defined. This concept is called the  -rank. For a detailed description of this rank concept, see [1].
-rank. For a detailed description of this rank concept, see [1].
For matrices, a low-rank approximation is optimal. An  -rank approximation of a tensor is not necessarily optimal. The higher-order orthogonal iteration (HOOI) is an optimization algorithm that improves the low-rank approximation. For HOOI, see [2].
-rank approximation of a tensor is not necessarily optimal. The higher-order orthogonal iteration (HOOI) is an optimization algorithm that improves the low-rank approximation. For HOOI, see [2].
Explanation of the Controls
"compression rate" slider: adjusts the ranks of the first and second dimensions 1–128; 128 means full-rank HOSVD (no compression), 1 means rank-(1,1,3)-HOSVD (maximum compression in this Demonstration)
"optimization" checkbox: controls whether the HOOI optimization algorithm (with 10 iterations) is executed or not
"test image" buttons: choose one of three different test images from Mathematica's ExampleData
References
[1] L. De Lathauwer, B. De Moor, and J. Vandewalle, "A Multilinear Singular Value Decomposition," SIAM Journal on Matrix Analysis and Applications, 21(4), 2000 pp. 1253–1278. doi:10.1137/S0895479896305696.
[2] L. De Lathauwer and J. Vandewalle, "Dimensionality Reduction in Higher-Order Signal Processing and Rank-(R1,R2,...,RN) Reduction in Multilinear Algebra," Linear Algebra and Its Applications, 391, 2004 pp. 31–55. doi:10.1016/j.laa.2004.01.016.
Permanent Citation