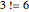Coloring 2D Metallic-Mean Quasicrystal Tilings with a Mesh-Based Method

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
This Demonstration provides code to automatically colour 2D quasicrystal tilings with a mesh-based method. it can also be used as an interactive example of the MeshRegion function and its related options introduced with release 11 of the Wolfram Language.
[more]
Contributed by: Jessica Alfonsi (June 2019)
(Padova, Italy)
Open content licensed under CC BY-NC-SA
Details
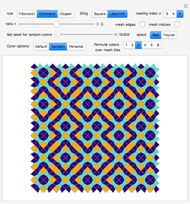
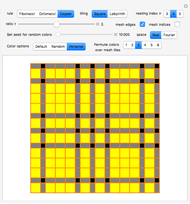
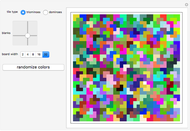
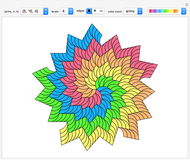
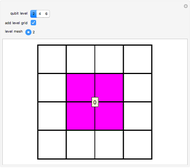
Snapshot 1: Square tiling of a 2D quasicrystal obtained from Fibonacci substitution rule, mesh indexing enabled and random set of colors
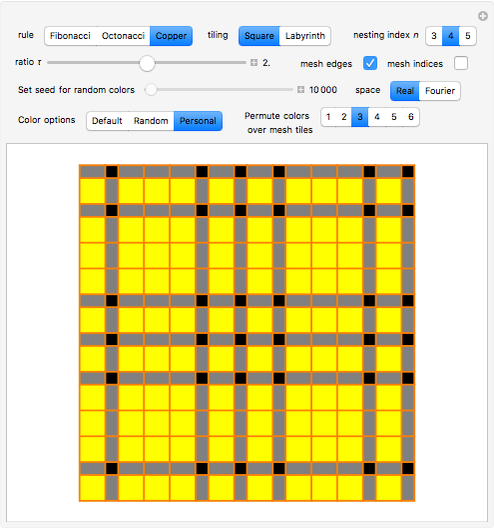
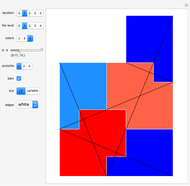
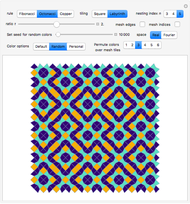
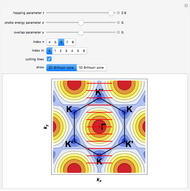
Snapshot 2: Square tiling of a 2D quasicrystal obtained from copper-mean substitution rule, mesh edge highlighting enabled and personal set of colors
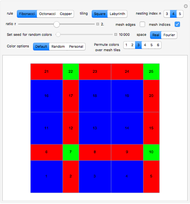
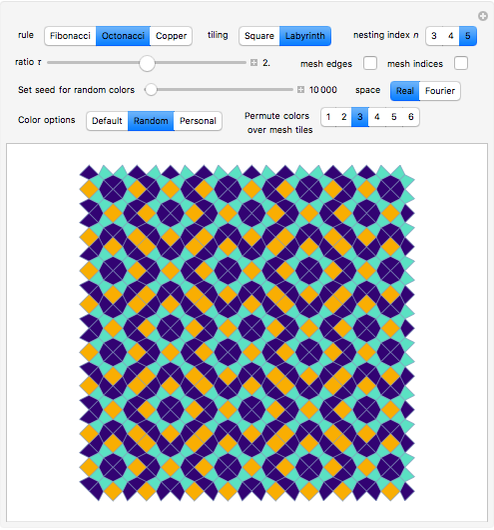
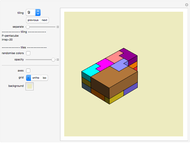
Snapshot 3: Labyrinth tiling of a 2D quasicrystal obtained from copper-mean substitution rule and default set of colors
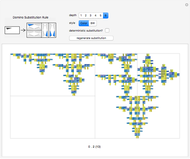
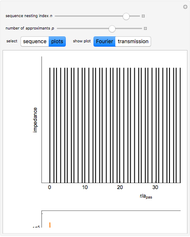
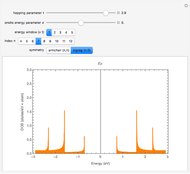
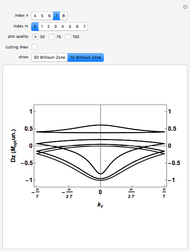
Snapshot 4: Fourier power map of mesh areas of 2D octonacci square tiling with indexed components and logarithmic color scale plot legend
Snapshot 5: Fourier power map of mesh areas of 2D labyrinth tiling from copper rule with with indexed components and logarithmic scale plot legend
Reference
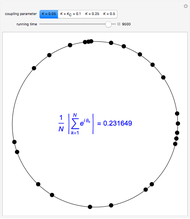
[1] U. Grimm and M. Schreiber, "Energy Spectra and Eigenstates of Quasiperiodic Tight-Binding Hamiltonians," in Quasicrystals: Structure and Physical Properties (H.-R. Trebin, ed.), Weinheim, Germany: Wiley-VCH, 2003 pp. 210–235. arxiv.org/abs/cond-mat/0212140.
[2] W. Steurer and S. Deloudi, "Tilings and Coverings", in Cristallography of Quasicrystals: Concepts, Methods and Structures, Springer-Verlag Berlin Heidelberg, Germany 2009 pp. 7-47
Snapshots
Permanent Citation