Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Commutative Matrices Associated with Vector Rotations

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

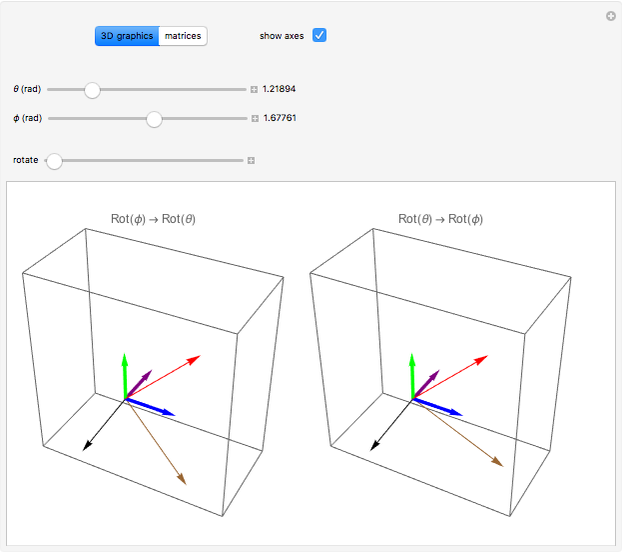
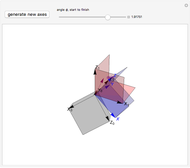
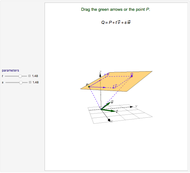
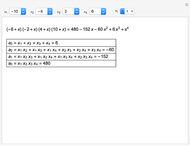
Rotations of vectors in three dimensions are, in general, not commutative. The one exception occurs when the two rotations occur in the same plane. In such cases, the commutative law for multiplication, , is valid.

[more]

Select the "3D graphics" button to see a graphic representation of the rotations; the "matrices" button shows the corresponding mathematical representation. The red dashed arrow marks the initial position and the brown arrow marks the position after the first rotation. The black arrow marks the position after the second rotation.

[less]

Contributed by: D. Meliga, A. Ratti and S. Z. Lavagnino (June 2019)
Additional contribution by: L. Lavagnino
Open content licensed under CC BY-NC-SA

Details

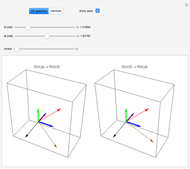
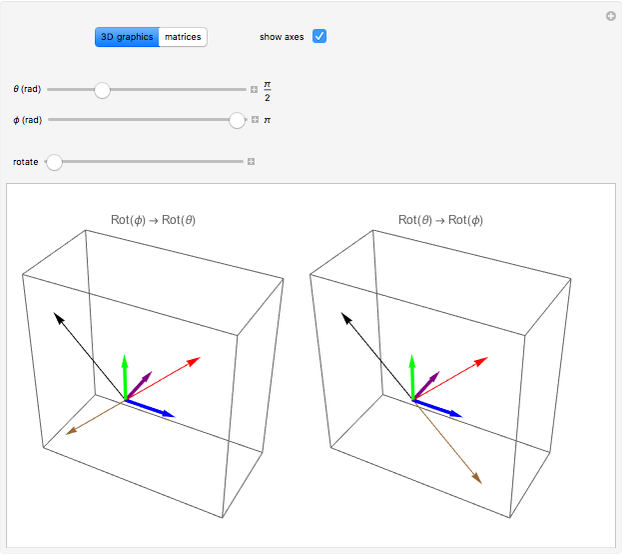
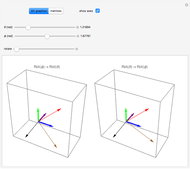
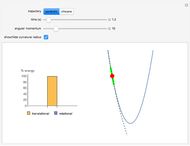
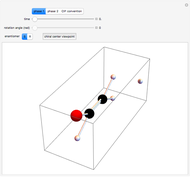
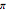Snapshot 1: The box on the right shows a rotation of following a rotation of , while the box on the left shows an initial rotation of and then a 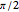rotation. Since the rotations are in the same plane, the final result is the same.

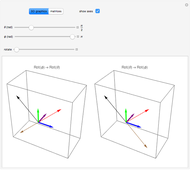
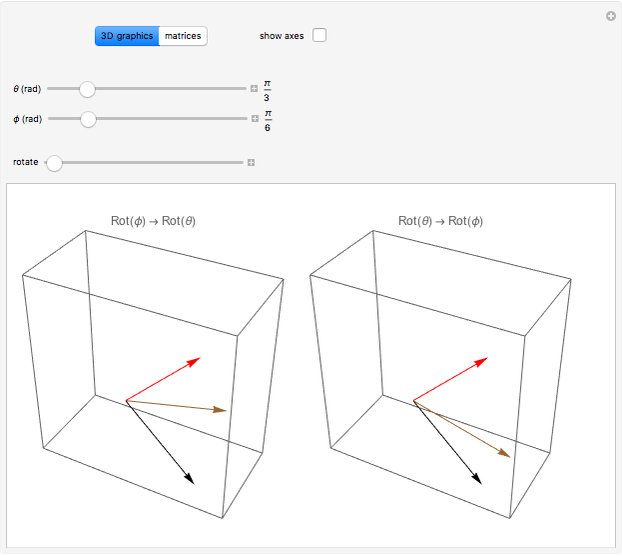
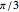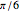Snapshot 2: The box on the right shows a rotation of following a rotation of , while the box on the left shows an initial rotation of and then a rotation. Again, the final result is the same.

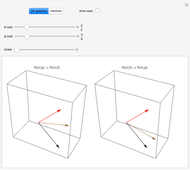
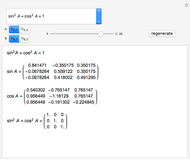
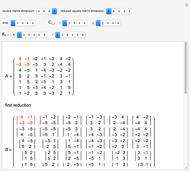
Snapshot 3: The rotation is written in matrix form; in this case, the matrix multiplication is commutative.

Reference

[1] D. J. Griffiths, Introduction to Quantum Mechanics, 2nd ed., Upper Saddle River, NJ: Pearson Prentice Hall, 2005.

Snapshots

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send