Comparing Four Methods of Numerical Inversion of Laplace Transforms (NILT)

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
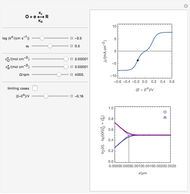
This Demonstration compares the efficiency of four methods for numerical inversion of Laplace transforms (NILT). The algorithms employed refer mainly to [1–3].
[more]
Contributed by: Claude Montella and Jean-Paul Diard (June 2015)
Open content licensed under CC BY-NC-SA
Snapshots
Details
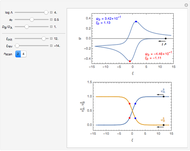
Numerical inversion of Laplace transforms (NILT) has become increasingly important in many application fields.
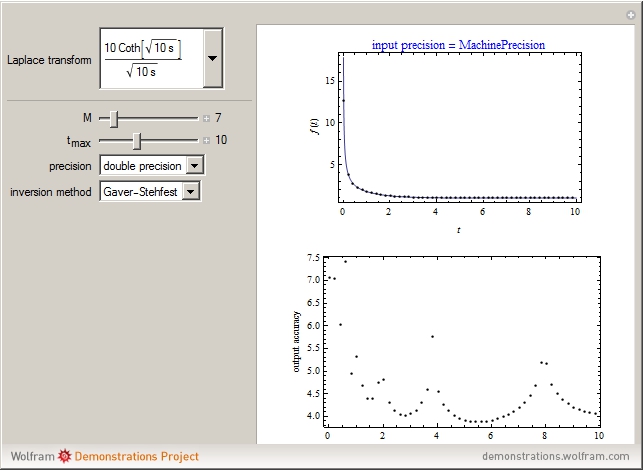
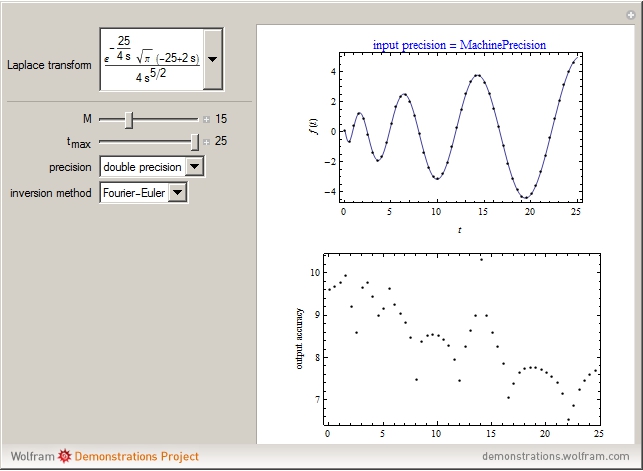
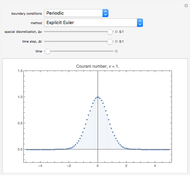
Four NILT methods are compared in this Demonstration, with special regard to some features of Laplace transformed functions, the time interval considered 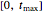 , the number of computation nodes in relation to the parameter
, the number of computation nodes in relation to the parameter 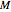 , and the computing mode (double precision or multi-precision).
, and the computing mode (double precision or multi-precision).
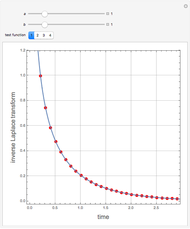
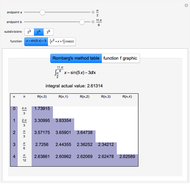
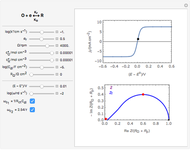
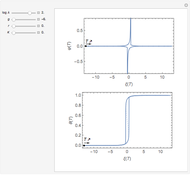
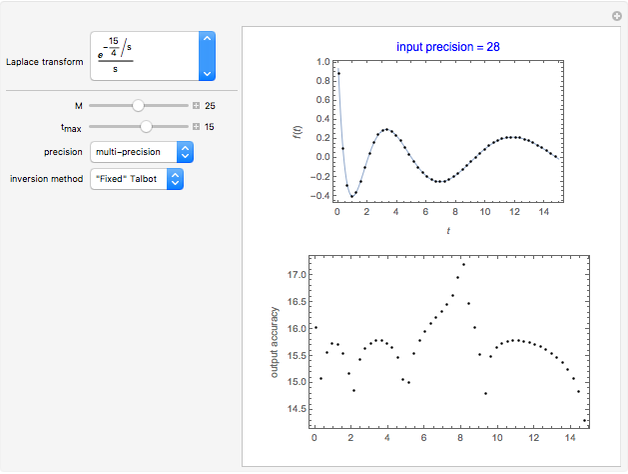
The inverse Laplace transform of the selected function (with Laplace variable  ) can be approximated numerically (shown as dots) using the selected NILT method together with the relevant algorithm. The exact inverse Laplace transform
) can be approximated numerically (shown as dots) using the selected NILT method together with the relevant algorithm. The exact inverse Laplace transform  is plotted as a full line. In some cases of very bad accuracy, computed data (dots) may stay outside the top graph.
is plotted as a full line. In some cases of very bad accuracy, computed data (dots) may stay outside the top graph.
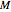 sets the number of Laplace transform values required for evaluation of one
sets the number of Laplace transform values required for evaluation of one  value, which is
value, which is 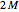 for the Gaver–Stehfest and Gaver–Wynn's rho methods,
for the Gaver–Stehfest and Gaver–Wynn's rho methods,  for the Fourier–Euler method, and
for the Fourier–Euler method, and 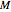 for the "fixed" Talbot method.
for the "fixed" Talbot method.
Numerical inversion can be performed in double-precision or multi-precision computation mode;  is the relative error.
is the relative error.
The output accuracy is 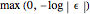 . The number of significant digits is the integer part of accuracy. Note that the input precision automatically switches to the multi-precision computing mode for Gaver–Wynn's rho algorithm because of its instability in double precision.
. The number of significant digits is the integer part of accuracy. Note that the input precision automatically switches to the multi-precision computing mode for Gaver–Wynn's rho algorithm because of its instability in double precision.
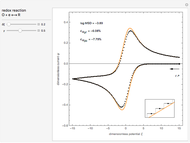
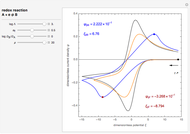
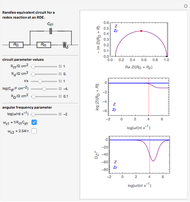
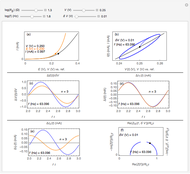
As far as we are concerned with electrochemical systems in our research field, some applications of NILT methods can be found, for example, in [5–7].
References
[1] J. Abate and W. Whitt, "A Unified Framework for Numerically Inverting Laplace Transforms," INFORMS Journal on Computing, 18(4), 2006 pp. 408–421. doi:10.1287/ijoc.1050.0137.
[2] P. P. Valkó and J. Abate, "Numerical Inversion of 2-D Laplace Transforms Applied to Fractional Diffusion Equations," Applied Numerical Mathematics, 53(1), 2005 pp. 73–88. doi:10.1016/j.apnum.2004.10.002.
[3] P. P. Valkó and J. Abate, "Comparison of Sequence Accelerators for the Gaver Method of Numerical Laplace Transform Inversion," Computers & Mathematics with Applications, 48(3–4), 2004 pp. 629–636. doi:10.1016/j.camwa.2002.10.017.
[4] A. M. Cohen, Numerical Methods for Laplace Transform Inversion, New York: Springer, 2007.
[5] C. Montella and J.-P. Diard, "New Approach of Electrochemical Systems Dynamics in the Time-Domain under Small-Signal Conditions. I. A Family of Algorithms Based on Numerical Inversion of Laplace Transforms," Journal of Electroanalytical Chemistry, 623(1), 2008 pp. 29–40. doi:10.1016/j.jelechem.2008.06.015.
[6] C. Montella and J.-P. Diard, "New Approach of Electrochemical Systems Dynamics in the Time Domain under Small-Signal Conditions. II. Modelling the Responses of Electrochemical Systems by Numerical Inversion of Laplace Transforms," Journal of Electroanalytical Chemistry, 625(2), 2009 pp. 156–164. doi:10.1016/j.jelechem.2008.10.025.
[7] C. Montella and R. Michel, "New Approach of Electrochemical Systems Dynamics in the Time Domain under Small-Signal Conditions. III. Discrimination between Nine Candidate Models for Analysis of PITT Experimental Data from 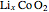 Film Electrodes," Journal of Electroanalytical Chemistry, 628(1–2), 2009 pp. 97–112. doi:10.1016/j.jelechem.2009.01.012.
Film Electrodes," Journal of Electroanalytical Chemistry, 628(1–2), 2009 pp. 97–112. doi:10.1016/j.jelechem.2009.01.012.
Permanent Citation